In diesem Artikel erklären wir dir, wie man den Begriff Cournotscher Punkt definiert. Wir gehen auf die Grundannahmen ein. Außerdem zeigen wir dir, wie man ihn grafisch darstellt. Und wir erläutern dir seine Bestimmung an einem Rechenbeispiel.
Definition
Cournotscher Punkt: Die gewinnmaximale Preis-Mengen-Kombination eines Monopolisten bezeichnet man als cournotschen Punkt. Punkt auf der Preis-Absatz-Funktion, wo sich Grenzerlös und Grenzkosten schneiden. Die gewinnmaximale Menge ergibt sich aus der Gewinnmaximierungsbedingung. Den dazugehörigen gewinnmaximalen Preis erhält man durch Einsetzen dieser Menge in die Preis-Absatz-Funktion.
Einen ersten Eindruck zur Vorgehensweise der Bestimmung des Cournot-Punktes vermittelt die folgende Abbildung. Sie übersetzt die Aussagen der Definition in eine Grafik.
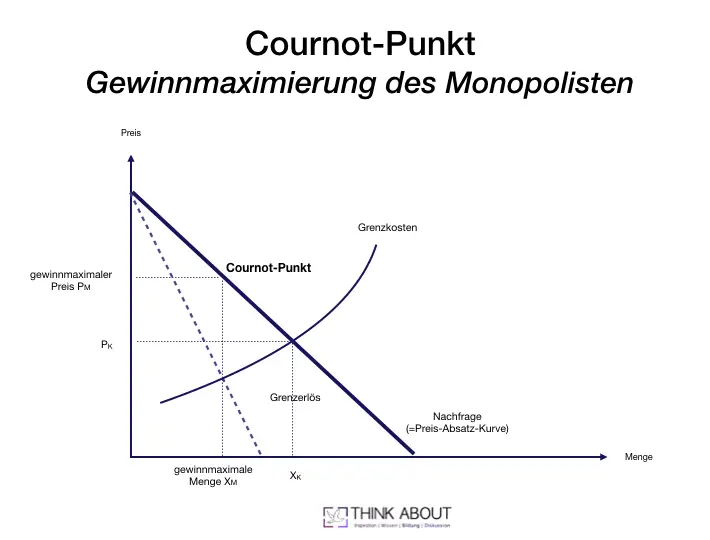
In den folgenden Abschnitten des Artikels gehen wir darauf ein, welche Formeln hinter den genannten Begrifflichkeiten stecken. Und wie man sie einerseits interpretiert und andererseits nutzen kann, um den Cournotschen Punkt zu berechnen.
Aus der Grafik wird deutlich, dass zur Bestimmung des Cournot-Punktes Kenntnisse zur Preissetzung des Monopolisten notwendig sind. Bzw. generell Kenntnisse zu den Begrifflichkeiten der mikroökonomischen Unternehmen- und Preistheorie unter Berücksichtigung verschiedener Marktformen. Diese Erläuterungen sind Gegenstand anderer Artikel auf thinkaboutgeny. In diesem Artikel setzen wir diese Kenntnisse weitestgehend als gegeben voraus und konzentrieren uns auf die notwendigen Erläuterungen, um den Cournotschen Punkt bestimmen zu können.
Aus der Grafik kann man für die nachfolgenden Erläuterungen folgende Punkte mitnehmen:
- Die Bestimmung des Cournotschen Punktes ist Bestandteil der Gewinnmaximierung des Monopolisten. D.h. es gelten die relevanten Annahmen zum Verlauf der Kurven und Optimierungsbedingungen.
- Für die Bestimmung des Cournotschen Punktes sind Kenntnisse über Verlauf der Preis-Absatz-Funktion und Kostenfunktion eines Monopolisten notwendig.
- Der Cournot Punkt liegt auf der Preis-Absatz Kurve. Er ist aber nicht der Schnittpunkt aus Grenzkosten und Grenzerlös. Anders formuliert: Der Cournot-Punkt selber ist kein Schnittpunkt, sondern ein Lageparameter.
Hintergrund und Bedeutung für die Volkswirtschaftslehre
Die Bestimmung des Cournotschen Punkt geht auf den Wissenschaftler Antoine Augustin Cournot zurück. Um die Bedeutung dieses Punktes einordnen zu können, sind einige Erläuterungen zum Werk von Cournot notwendig. Insgesamt betrachtet kann man Cournot als Begründer der neoklassischen Preistheorie bezeichnen. Sein Name begegnet Studierenden im ersten Studienjahr in den Grundlagenveranstaltungen zur Mikroökonomie. Während die Bezeichnung des Cournotschen Punktes in den Ausführungen zur Preissetzung des Monopolisten in der Regel vom Lehrbuch abhängt, ist sein Name untrennbar mit den Ausführungen zum Oligopol verbunden (Stichwort: Cournot-Modell bzw. Cournot-Wettbewerb).
Als früher Neoklassiker befasste sich Cournot mit mikroökonomischen Fragestellungen. Im Mittelpunkt seiner Analysen stand der Umfang der Produktion von Unternehmen. Bei gegebener Nachfrage durch die Konsumenten wird der Produktionsumfang durch den Preis bestimmt. Deshalb auch die Bezeichnung Preistheorie. Cournot berücksichtigte hierbei auch explizit die Marktform, wobei er zwischen Polypol, Monopol und Oligopol in den Auswirkungen unterschied. Grundlage für seine Analysen waren die von ihm entwickelten Angebot-Nachfrage-Darstellungen. Der Cournotsche Punkt ist nun ein Teil seiner Ausarbeitungen zum Monopol.
Die Erkenntnisse von Cournot setzten sich nur langsam durch. Erst durch die Aufnahme seiner Analysemethoden und Erkenntnisse in die Arbeiten anderer Neoklassiker fanden sie Verbreitung.
Cournotscher Punkt: Grafische und ökonomische Erklärung
1. Erklärung Cournotscher Punkt
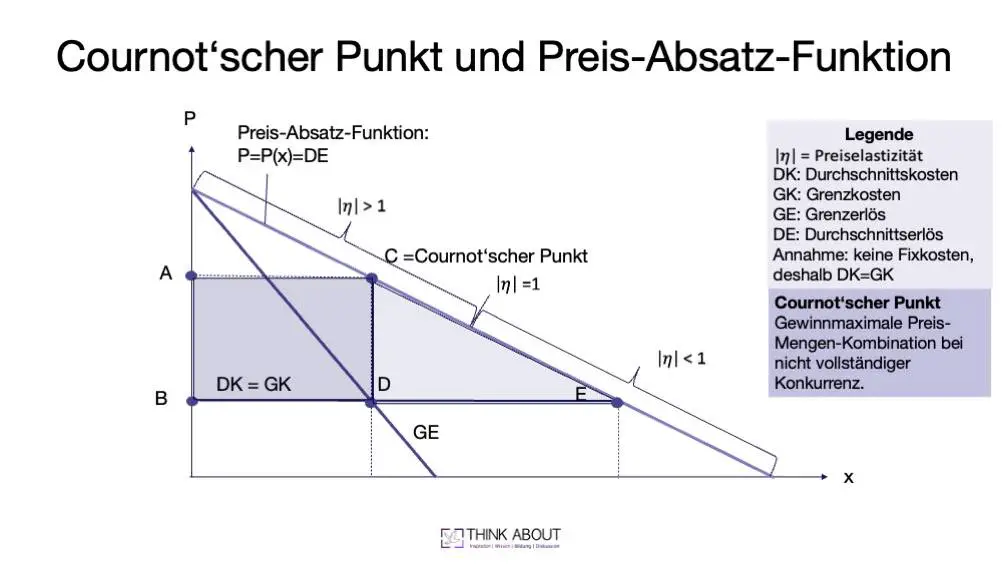
Diese Grafik ist sehr ähnlich wie die vorherige Abbildung zum Cournotschen Punkt aufgebaut. Wir haben die Preis-Absatz-Funktion allerdings um Informationen zur Preiselastizität ergänzt. Außerdem gehen wir in dieser Grafik davon aus, dass dem Monopolisten keine Fixkosten entstehen. Wenn eine Kostenfunktion nur variable Kosten enthält, entsprechen die Durchschnittskosten immer den Grenzkosten.
Zur Bestimmung sind nun Kenntnisse zum Verlauf der Preis-Absatz-Funktion, der Grenz-Erlös-Funktion, sowie der Kosten- und Grenzkosten-Funktion notwendig.
Hier ist zu beachten, dass der Monopolist als alleiniger Anbieter kein Preisnehmer ist. Er sieht sich im Gegensatz zu anderen Marktformen der gesamten Marktnachfrage alleine gegenüber. Seine Preis-Absatz-Funktion hat deshalb einen negativen Verlauf.
Gewinnmaximierung des Monopolisten:
Grenzerlös = Grenzkosten
In der Grafik wird dieser gewinnmaximale Punkt durch Punkt D dargestellt. Dieser Punkt bestimmt die gewinnmaximale Verkaufsmenge. Der Monopolist kann nun aber den Preis selber setzen. D.h. er kann die Menge in Abhängigkeit der Preis-Absatz-Funktion zu einem höheren Preis verkaufen. Dies ist der Punkt C, der auch der Cournotsche Punkt ist.
Der Cournotsche Punkt bestimmt damit das Gewinnmaximum. Interessant ist nun die Beziehung zwischen Gewinnhöhe und Preiselastizität. Das Gewinnmaximum, und damit der Cournot-Punkt, liegt immer im elastischen Bereich der Preis-Absatz- bzw. Nachfragefunktion. Im unelastischen Bereich verringern sich die Gewinne, da der Abstand zwischen Erlösen und Kosten immer geringer wird. Ab einem zu bestimmenden Punkt werden die Gewinne dann sogar negativ. In der Grafik wäre dies exemplarisch Punkt E.
2. Formeln zur Bestimmung des Cournotschen Punktes
Der Cournotsche Punkt stelle das Gewinnmaximum dar. Die Gewinnmaximierung erfolgt über den Grenzgewinn. Der Grenzgewinn ist die 1. Ableitung des Gewinns und er wird gleich null gesetzt.
Es gilt:
dG(x)/dx = 0
Um zu diesem Ergebnis zu gelangen, benötigen wir Informationen und Formeln zum Erlös und zu den Kosten:
Gewinn = Erlös – Kosten
Der Gewinn ergibt sich aus Erlös abzüglich Kosten. Alle Faktoren sind von der Menge der produzierten und verkauften Güter abhängig.
G (x) = E (x) - K(x) = 0
Der Grenzgewinne ergibt sich damit aus dem Grenzerlös abzüglich Grenzkosten:
dG(x)/dx = dE(x)/dx – dK(x)/dx = 0
Da der Grenzgewinn gleich Null ist, kann die Gleichung umformuliert werden:
dE(x)/dx – dK(x)/dx = 0
Hieraus folgt, dass der Grenzerlös den Grenzkosten im Optimum entspricht:
dE(x)/dx = dK(x)/dx = 0
Hiermit haben wir mathematisch gezeigt, was wir vorher verbal und grafisch dargestellt haben: Die gewinnmaximale Verkaufsmenge liegt dort, wo der Grenzerlös den Grenzkosten entspricht.
Zum Cournotschen Punkt gelangt man, wenn die sich aus der Formel ergebende gewinnmaximale Menge in die Preis-Absatz-Funktion einsetzt und diese nach dem Preis P auflöst. Hieraus ergibt sich der Cournot-Punkt bzw. der gewinnmaximale Preis.
Bedingungen für das Cournot-Modell und den Cournotschen Punkt
Aus den vorherigen Erläuterungen ergeben sich mehre Bedingungen, die erfüllt sein müssen, damit man in einem Monopol einen Cournotschen Punkt berechnen kann. Die Voraussetzungen bauen darauf auf, dass für das allein produzierende Unternehmen vollkommene Marktbedingungen vorliegen:
Keine Preisdiskriminierung: Das monopolistische Unternehmen achtet nicht auf die individuelle Zahlungsbereitschaft der Konsumenten. Für alle Konsumenten existiert derselbe Preis.
Keine Kapazitätsbeschränkungen: Begrenzungen von Produktionsfaktoren und Einfluss von Faktorpreisen werden ausgeklammert. Wenn genügend Nachfrage nach den Gütern besteht, kann der Monopolist seine Produktion bis ins Unendliche ausweiten und seine Güter verkaufen.
Rationalität: Das monopolistische Unternehmen verhält sich rational. Es ist das Ziel des Monopolisten seinen Gewinn zu maximieren.
Preis-Absatz- und Kostenfunktion: Die beiden Funktionen stellen die Grundlage für die Berechnung des Cournotschen Punktes dar. Sie müssen deshalb bekannt sein.
Übersicht Berechnung Cournotscher Punkt

Schritt 1: Überblick Preis-Absatz- und Kostenfunktion
Preis-Absatzfunktion: p=p(x) -> a - bx
Kostenfunktion: K= Kf + Kv (x) -> a + bx
Schritt 2: Herleitung der Erlösfunktion
Erlösfunktion: E(x) = p(x) * x = (a - x) * x = ax - x2
Schritt 3: Bestimmung Grenzumsatz und Grenzkosten
Grenzumsatz: dE(x)/x = a - 2x
Grenzkosten: dK(x)/x = b
Ableiten der Erlösfunktion bzw. Kostenfunktion aus Schritt 2 nach x.
Schritt 4: Berechnung Gewinnmaximale Menge und Cournot Preis und Cournotscher Punkt
dE(x)/dx = dK(x)/dx = 0
a - 2x = b
Auflösen nach x:
-2bx = b - a
Schritt 5: Berechnung Gewinnmaximum
Rechenbeispiel Cournotscher Punkt
Schritt 1: Übersicht
Preis-Absatz-Funktion: p = 16 - x
Kosten-Funktion: K(x) = 10 + 4x
Schritt 2: Erlösfunktion
Erlös-Funktion: E(x) = x * p = x * (16 - x) = 16x – x2
Hinweis: Oft wird statt Erlös von Umsatz gesprochen.
Schritt 3: Grenzerlös und Grenzkosten
Grenzumsatz: dE(x)/x = 16 - 2x
Grenzkosten: dK(x)/x = 4
Schritt 4: Berechnung Gewinnmaximale Menge und Cournot Preis und Cournotscher Punkt
dE(x)/dx = dK(x)/dx = 0
Funktion einsetzen:
16 - 2x = 4
Nach x auflösen ergibt die gewinnmaximale Menge:
X* = 6
Berechnung des Gewinnmaximalen Preises:
X* wird in die Preis-Absatz-Funktion eingesetzt:
Preis-Absatz-Funktion: p = 16 - x
P* = 16 - 6 = 10
Ergebnis: Der gewinnmaximale Preis beträgt 10.
Der Cournotsche Punkt liegt damit auf der Preis-Absatz-Funktion an der Stelle (x*= 6 und p*= 10).
Schritt 5: Berechnung Gewinnmaximum
Abschließend kann man noch den sich hieraus ergebenden Gewinn berechnen. Dazu einfach die berechneten Werte in die Erlös- und Kosten-Funktion einsetzen und die erhaltenen Kosten von den Erlösen abziehen:
G (x) = E(x) – K(x)
E (x) = x * p = 6 * 10 = 60
K (x) = 10 + 4x = 10+ 4 * 6 = 34
Ergebnis: Der Erlös beträgt damit 60 Geldeinheiten und die Kosten 34 Geldeinheiten.
Hieraus ergibt sich ein maximaler Gewinn von 26 Geldeinheiten:
Gewinn: 60 – 34 = 26
Um herauszufinden, ob es sich bei diesem Wert tatsächlich um das Gewinnmaximum handelt, berechnet man die zweite Ableitung der Gewinnfunktion. Ist sie negativ, ist alles in Ordnung. Als Ergebnis kommt – 4 heraus (da man die zweite Ableitung Kostenfunktion von der zweiten Ableitung der Erlösfunktion abzieht).
