Die Grenzrate der technischen Substitution stellt das Austauschverhältnis zweier Produktionsfaktoren dar, bei konstantem Produktionsniveau. In diesem Artikel erklären wir euch Definition, Interpretation und Berechnung der Grenzrate der technischen Substitution.
Definition Grenzrate der technischen Substitution einfach erklärt
Grenzrate der technischen Substitution (GRTS): Austauschverhältnis zweier Produktionsfaktoren. Sie beschreibt die prozentuale Änderung des Einsatzes eines Produktionsfaktors, wenn der Einsatz eines anderen Faktors um einen Prozentpunkt verändert wird, um die Gesamtproduktion konstant zu halten.
Die Grenzrate der technischen Substitution (GRTS) ist ein Konzept aus der Mikroökonomie und beschreibt die Rate, mit der eine Produktionsfaktorart durch eine andere ersetzt werden kann, ohne dass sich die Gesamtproduktion ändert.
Konkret gibt die GRTS an, um wie viel Prozent der Einsatz eines Faktors reduziert werden kann, wenn der Einsatz des anderen Faktors um einen Prozentpunkt erhöht wird, damit die Produktion konstant bleibt. Die GRTS hängt dabei von der Produktionsfunktion, also der Art und Weise, wie die Faktoren miteinander kombiniert werden können, ab. Unterschiedliche Produktionsfunktionen können unterschiedliche GRTS-Werte für dieselbe Kombination von Faktoren liefern.
Die GRTS ist somit ein wichtiger Faktor für die Entscheidung von Unternehmen, wie sie ihre Produktionsfaktoren einsetzen, um die Produktion zu maximieren oder Kosten zu minimieren. Eine hohe GRTS bedeutet, dass die Faktoren leicht austauschbar sind, während eine niedrige GRTS darauf hinweist, dass die Faktoren spezialisiert sind und schwer zu ersetzen sind.
Formel der Grenzrate der technischen Substitution
Die Formel für die Grenzrate der technischen Substitution (GRTS) lautet:
GRTS_{AB} = (dA/dQ)/(dB/dQ)
Hierbei steht A für einen Produktionsfaktor und B für einen anderen Produktionsfaktor. dA/dQ und dB/dQ sind partielle Ableitungen der Produktionsfunktion nach A bzw. B.
Die GRTS_{AB} gibt an, um wie viel Einheiten des Faktors B reduziert werden kann, wenn eine Einheit des Faktors A erhöht wird, während das Produktionsniveau konstant bleibt. Sie gibt also das Verhältnis der Mengenänderungen zwischen den beiden Faktoren wieder, die notwendig sind, um den gleichen Output zu erzielen.
Interpretation der Grenzrate der technischen Substitution
Die Grenzrate der technischen Substitution gibt an, wie leicht oder schwer es für ein Unternehmen ist, die Verwendung eines Produktionsfaktors durch einen anderen Faktor zu ersetzen, um die Produktion aufrechtzuerhalten. Eine hohe GRTS bedeutet, dass die Faktoren leicht austauschbar sind, während eine niedrige GRTS darauf hinweist, dass die Faktoren spezialisiert sind und schwer zu ersetzen sind.
Ein Beispiel für eine hohe GRTS wäre die Herstellung von Büchern. Die Verwendung von menschlicher Arbeitskraft und Maschinen kann leicht variiert werden, um die Produktion aufrechtzuerhalten. Wenn zum Beispiel der Einsatz von Maschinen erhöht wird, kann die Anzahl der Arbeiter reduziert werden, um die gleiche Menge an Büchern herzustellen.
Ein Beispiel für eine niedrige GRTS wäre die Herstellung von hoch spezialisierten Produkten wie Flugzeugmotoren. Wenn beispielsweise der Einsatz von erfahrenen Ingenieuren reduziert wird, um die Anzahl der Arbeiter zu erhöhen, kann dies die Qualität der Produktion beeinträchtigen und zu höheren Kosten führen, um Fehler zu beheben.
Eigenschaften der Grenzrate der technischen Substitution
Die GRTS ist ein wichtiges Konzept in der Mikroökonomie und wird häufig verwendet, um die Produktionsstrategien von Unternehmen zu analysieren und die Effizienz der Faktorverwendung zu bewerten.
Zusammenhang zwischen Produktionsfunktion und Grenzrate der technischen Substitution
Die Grenzrate der technischen Substitution (GRTS) hängt eng mit der verwendeten Produktionsfunktion zusammen, da sie angibt, wie leicht oder schwer es ist, einen Produktionsfaktor durch einen anderen zu ersetzen, um die Gesamtproduktion zu halten.
Es gibt verschiedene Produktionsfunktionen, die die Art und Weise beschreiben, wie die Faktoren miteinander kombiniert werden können, um eine bestimmte Menge an Output zu produzieren. Die drei wichtigsten Funktionen sind die lineare Funktion, die Cobb-Douglas-Funktion und die Leontief-Funktion.
- Die lineare Funktion hat eine konstante Grenzrate der technischen Substitution, da sie eine lineare Beziehung zwischen den Produktionsfaktoren annimmt. Das bedeutet, dass die Faktoren in einem festen Verhältnis zueinanderstehen und gleich leicht austauschbar sind. Ein Beispiel für eine lineare Funktion wäre die Herstellung von Holzpaletten, bei der der Einsatz von Holz und Nägeln in einem konstanten Verhältnis zueinandersteht.
- Die Cobb-Douglas-Funktion hingegen hat eine fallende Grenzrate der technischen Substitution, da sie eine elastische Beziehung zwischen den Produktionsfaktoren annimmt. Das bedeutet, dass die Faktoren leicht austauschbar sind, aber nicht in gleichem Maße. Ein Beispiel für eine Cobb-Douglas-Funktion wäre die Produktion von Smartphones, bei der eine höhere Anzahl von Arbeitern und Maschinen eine höhere Produktion ermöglichen, aber nicht in gleicher Weise.
- Die Leontief-Funktion hat eine unendlich hohe Grenzrate der technischen Substitution, da sie eine feste Beziehung zwischen den Produktionsfaktoren annimmt. Das bedeutet, dass die Faktoren perfekt miteinander komplementär sind und nicht ersetzt werden können, ohne die Produktion zu beeinträchtigen. Ein Beispiel für eine Leontief-Funktion wäre die Herstellung von Autoreifen, bei der eine bestimmte Menge an Gummi und Stahl benötigt wird, um einen Reifen zu produzieren, und keine der Zutaten durch eine andere ersetzt werden kann.
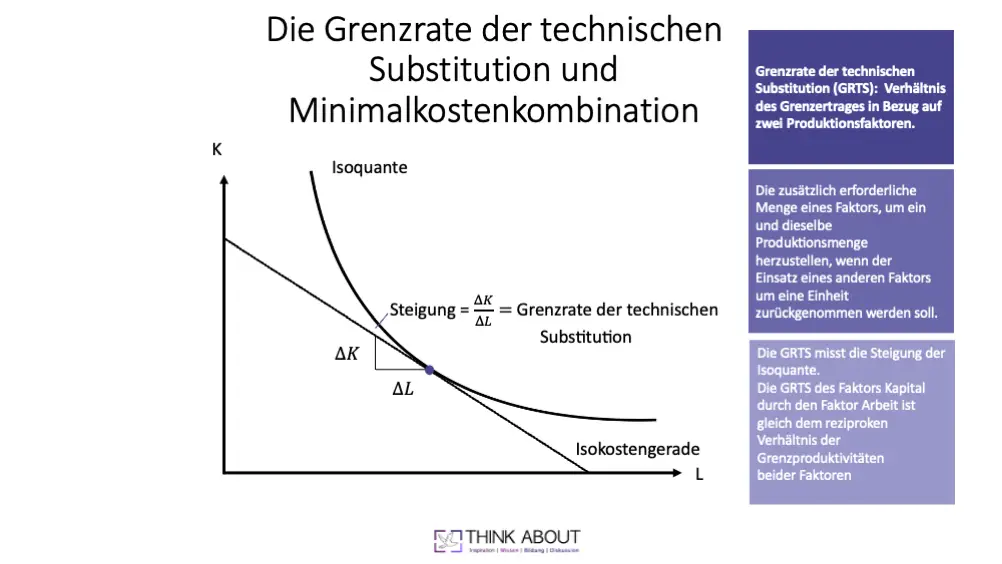
Was ist der Zusammenhang zwischen der Isoquante und der Grenzrate der technischen Substitution?
Die Isoquante ist eine Kurve, die alle Kombinationen von Produktionsfaktoren darstellt, die das gleiche Produktionsniveau ergeben.
Die Grenzrate der technischen Substitution (GRTS) gibt hingegen an, wie leicht oder schwer es ist, einen Produktionsfaktor durch einen anderen zu ersetzen, um das Produktionsniveau aufrechtzuerhalten.
Der Zusammenhang zwischen der Isoquante und der GRTS ist auf folgende Weise gegeben: Die Steigung der Isoquante an einem bestimmten Punkt entspricht der negativen GRTS an diesem Punkt. Mit anderen Worten, die GRTS gibt die Änderungsrate an, mit der ein Faktor durch einen anderen ersetzt werden kann, während die Isoquante die Menge an Faktorkombinationen angibt, die das gleiche Produktionsniveau ergeben.
Wenn die GRTS hoch ist, d.h, wenn ein Produktionsfaktor relativ leicht durch einen anderen ersetzt werden kann, dann wird die Isoquante flach sein, d.h es gibt viele Kombinationen von Produktionsfaktoren, die dasselbe Produktionsniveau ergeben. Wenn die GRTS hingegen niedrig ist, d.h, wenn ein Faktor schwer durch einen anderen ersetzt werden kann, dann wird die Isoquante steiler sein, d.h es gibt nur wenige Kombinationen von Produktionsfaktoren, die dasselbe Produktionsniveau ergeben.
Insgesamt ist die GRTS ein wichtiges Konzept, um zu verstehen, wie Unternehmen Faktoren substituieren und die Produktionseffizienz verbessern können, während die Isoquante eine nützliche grafische Darstellung der Produktionsmöglichkeiten darstellt.
Zusammenhang Grenzprodukt und Grenzrate der technischen Substitution
Das Grenzprodukt ist definiert als die Veränderung der Produktionsmenge, die durch eine zusätzliche Einheit eines Produktionsfaktors (z.B. Arbeit oder Kapital) erzielt wird.
Die Grenzrate der technischen Substitution (GRTS) hingegen beschreibt die Rate, mit der ein Produktionsfaktor durch einen anderen substituiert werden kann, um das gleiche Produktionsergebnis aufrechtzuerhalten.
Es gibt einen engen Zusammenhang zwischen diesen beiden Konzepten. Wenn der Einsatz eines Produktionsfaktors erhöht wird, kann dies entweder durch eine Erhöhung des Einsatzes dieses Faktors selbst oder durch eine Erhöhung des Einsatzes eines anderen Faktors kompensiert werden. Die GRTS gibt an, wie viel von einem Produktionsfaktor durch einen anderen ersetzt werden kann, um das gleiche Produktionsergebnis aufrechtzuerhalten.
Die GRTS ist auch eng mit dem Grenzprodukt verknüpft. Wenn der Einsatz eines Produktionsfaktors erhöht wird, steigt das Grenzprodukt zuerst an, aber irgendwann nimmt es ab, da die Produktionsfaktoren nicht unbegrenzt substituierbar sind. Die GRTS erreicht ihren maximalen Wert, wenn das Grenzprodukt des zu substituierenden Faktors gleich dem Grenzprodukt des Ersatzfaktors ist.
In anderen Worten, der maximale Wert der GRTS wird erreicht, wenn die zusätzliche Menge des zu ersetzenden Faktors genau durch die Menge des ersetzenden Faktors ersetzt werden kann, ohne dass sich das Gesamtprodukt ändert. Wenn sich das Grenzprodukt des zu ersetzenden Faktors ändert, ändert sich auch die GRTS entsprechend.
Bedeutung und Entwicklung der Grenzrate der technischen Substitution in der Mikroökonomie
Das Konzept der Grenzrate der technischen Substitution wurde von dem Ökonomen Joan Robinson entwickelt. Es wurde erstmals in ihrem Buch „The Economics of Imperfect Competition“ im Jahr 1933 vorgestellt.
In der Mikroökonomik hat die Grenzrate der technischen Substitution eine zentrale Bedeutung bei der Untersuchung der Produktionstechnologie und der Bestimmung von optimalen Faktorkombinationen. Sie gibt an, wie leicht oder schwer es für ein Unternehmen ist, die Verwendung eines Produktionsfaktors durch einen anderen zu ersetzen, um die Gesamtproduktion aufrechtzuerhalten.
Die GRTS hat auch wichtige Anwendungen in der Analyse von Marktstrukturen, insbesondere von oligopolistischen und monopolistischen Märkten. In solchen Märkten können Unternehmen ihre Produktionstechnologie nutzen, um den Marktzugang von Konkurrenten zu behindern oder ihre eigene Marktmacht zu erhöhen. Die GRTS hilft dabei, die Reaktion von Unternehmen auf Änderungen der Faktorpreise und die Auswirkungen von Technologieinnovationen auf die Wettbewerbsbedingungen zu verstehen.
Konkret hilft die GRTS Unternehmen, die beste Kombination von Produktionsfaktoren zu finden, um ihre Produktion zu maximieren, ohne dabei die Kosten zu erhöhen. Die GRTS ist auch nützlich, um zu verstehen, wie sich Faktorpreise und technologischer Fortschritt auf die Produktion und den Wettbewerb in verschiedenen Märkten auswirken.
Insgesamt ist die GRTS ein wichtiges Konzept für die Analyse der Produktion und der Wettbewerbsbedingungen in der Mikroökonomie und für Unternehmen bei der Entscheidung, wie sie ihre Produktion effizienter gestalten können.
Wie berechnet und zeichnet man die Grenzrate der technischen Substitution?
1. Berechnung der Grenzrate der technischen Substitution
Die Grenzrate der technischen Substitution (GRTS) wird berechnet, indem man die partielle Ableitung des Outputs (Q) nach einem Produktionsfaktor (z.B. Arbeit L) durch die partielle Ableitung des Outputs nach einem anderen Produktionsfaktor (z.B. Kapital K) teilt. Formal lautet die GRTS:
GRTS_{LK} = (dK/dQ)/(dL/dQ)
Das bedeutet, dass man zuerst die partielle Ableitung des Outputs nach K und L bilden muss, um dann das Verhältnis der beiden Ableitungen zu bilden.
Hier sind die Schritte zur Berechnung der technischen Substitution:
- Identifiziere die beiden Produktionsfaktoren, zwischen denen die Substitution stattfinden soll.
- Bestimme die Produktionsfunktion, die angibt, wie die Produktionsmenge von den eingesetzten Faktormengen abhängt.
- Berechne die partielle Ableitung der Produktionsfunktion nach jedem Produktionsfaktor, um die Grenzproduktivität jedes Faktors zu erhalten. Das Grenzprodukt gibt an, wie viel die Produktionsmenge zunimmt, wenn die eingesetzte Menge des Faktors um eine Einheit erhöht wird.
- Berechne die Grenzrate der technischen Substitution (GRTS), indem du die partielle Ableitung des Outputs nach dem einen Faktor durch die Ableitung des Outputs nach dem anderen Faktor teilst. Das Verhältnis gibt an, wie viel Einheiten des einen Faktors durch eine Einheit des anderen Faktors ersetzt werden können, um die gleiche Produktionsmenge aufrechtzuerhalten.
- Interpretiere das Ergebnis der GRTS-Berechnung. Ein Wert größer als 1 bedeutet, dass die Faktoren substituierbar sind, während ein Wert kleiner als 1 bedeutet, dass die Faktoren komplementär sind.
Wiederhole ggf. den Berechnungsprozess für verschiedene Kombinationen von Faktoren, um das Substitutionsverhalten der Produktionsfunktion zu untersuchen.
2. Beispiele zur Berechnung der Grenzrate der technischen Substitution
Nachdem wir nun das generelle Vorgehen zur Berechnung der GRTS kennen, zeigen wir euch an den bekanntesten Produktionsfunktionen beispielhaft, wie man diese Schritte umsetzt.
Beispiel 1: Cobb-Douglas. Produktionsfunktion und Grenzrate der technischen Substitution
Angenommen, wir haben eine Cobb-Douglas-Produktionsfunktion mit folgenden Parametern:
Q = 10 * K^{0,5} * L^{0,5}
Um die GRTS zwischen Arbeit und Kapital zu berechnen, müssen wir die partiellen Ableitungen der Produktionsfunktion nach K und L bilden:
dQ/dK = 5 * K^{-0,5} * L^{0,5}
dQ/dL = 5 * K^{0,5} * L^{-0,5}
Die GRTS zwischen Arbeit und Kapital (GRTS_{LK}) lautet:
GRTS_{LK} = (dK/dQ) / (dL/dQ) = (5 * K^{-0,5} * L^{0,5}) / (5 * K^{0,5} * L^{-0,5}) = (K/L)
Angenommen, wir haben K = 25 und L = 100, dann ist die GRTS_{LK}:
GRTS_{LK} = K/L = 25/100 = 0,25Das bedeutet, dass ein Anstieg der Arbeit um 1 % eine Reduktion des Kapitaleinsatzes um 0,25 % erfordert, um die Produktion auf dem gleichen Niveau zu halten.
Beispiel 2: CES-Produktionsfunktion und Grenzrate der technischen Substitution
Die CES-Funktion (constant elasticity of substitution function) ist eine spezielle Form einer Produktionsfunktion in der Mikroökonomie. Sie beschreibt, wie viel Output produziert wird, wenn man bestimmte Mengen an Produktionsfaktoren wie Kapital und Arbeit kombiniert. Im Gegensatz zu anderen Produktionsfunktionen erlaubt die CES-Funktion jedoch eine konstante Elastizität der Substitution zwischen den Produktionsfaktoren, d. h. sie gibt an, wie leicht die Produktionsfaktoren substituiert werden können.
Die CES-Funktion hat die Form:
Q = [a(K^rho) + (1-a)(L^rho)]^(1/rho)
wobei Q die produzierte Menge, K das Kapital, L die Arbeit, a der Anteil des Kapitals an der Gesamtproduktion, rho der Elastizitätsparameter der Substitution und r der Skalierungsparameter sind.
Angenommen, wir haben eine CES-Produktionsfunktion mit folgenden Parametern:
Q = (0.3K^-0.5 + 0.7L^-0.5)^(-2)
Um die GRTS zwischen Arbeit und Kapital zu berechnen, müssen wir die partiellen Ableitungen der Produktionsfunktion nach K und L bilden:
dQ/dK = 0.3Q * K^(-1.5) / (0.3K^-0.5 + 0.7L^-0.5)^3
dQ/dL = 0.7Q * L^(-1.5) / (0.3K^-0.5 + 0.7L^-0.5)^3
Die GRTS zwischen Arbeit und Kapital (GRTS_{LK}) lautet:
GRTS_LK = (dK/dQ) / (dL/dQ) = (0.3Q * K^(-1.5) / (0.3K^-0.5 + 0.7L^-0.5)^3) / (0.7Q * L^(-1.5) / (0.3K^-0.5 + 0.7L^-0.5)^3) = (K/L)
Angenommen, wir haben K = 16 und L = 64, dann ist die GRTS_{LK}:
GRTS_{LK} = K/L = 16/64 = 0,25
Das bedeutet, dass ein Anstieg der Arbeit um 1 % eine Reduktion des Kapitaleinsatzes um 0,25 % erfordert, um die Produktion auf dem gleichen Niveau zu halten.
Beispiel 3: Lineare Produktionsfunktion und Grenzrate der technischen Substitution
Wir haben eine lineare Produktionsfunktion mit folgender Form:
Q = 2K + 3L
Um die GRTS zwischen Arbeit und Kapital zu berechnen, müssen wir die partiellen Ableitungen der Produktionsfunktion nach K und L bilden:
dQ/dK = 2
dQ/dL = 3
Die GRTS zwischen Arbeit und Kapital (GRTS_{LK}) lautet:
GRTS_{LK} = (dK/dQ) / (dL/dQ) = 2/3
Das bedeutet, dass ein Anstieg der Arbeit um 1 % eine Reduktion des Kapitaleinsatzes um 2/3 % erfordert, um die Produktion auf dem gleichen Niveau zu halten.
Beispiel 4: Leontief-Produktionsfunktion und Grenzrate der technischen Substitution
Angenommen, wir haben eine Leontief-Produktionsfunktion mit folgenden Parametern:
Q = min {20K, 15L}
Um die GRTS zwischen Arbeit und Kapital zu berechnen, bilden wir wieder die partiellen Ableitungen der Produktionsfunktion nach K und L:
dQ/dK = 20, wenn 20K < 15L
dQ/dK = 0, wenn 20K > 15L
dQ/dL = 15, wenn 15L < 20K
dQ/dL = 0, wenn 15L > 20K
Die GRTS zwischen Arbeit und Kapital (GRTS_{LK}) ist in diesem Fall nicht definiert, da die partiellen Ableitungen nicht stetig sind.
3. Grafische Darstellung der Grenzrate der technischen Substitution
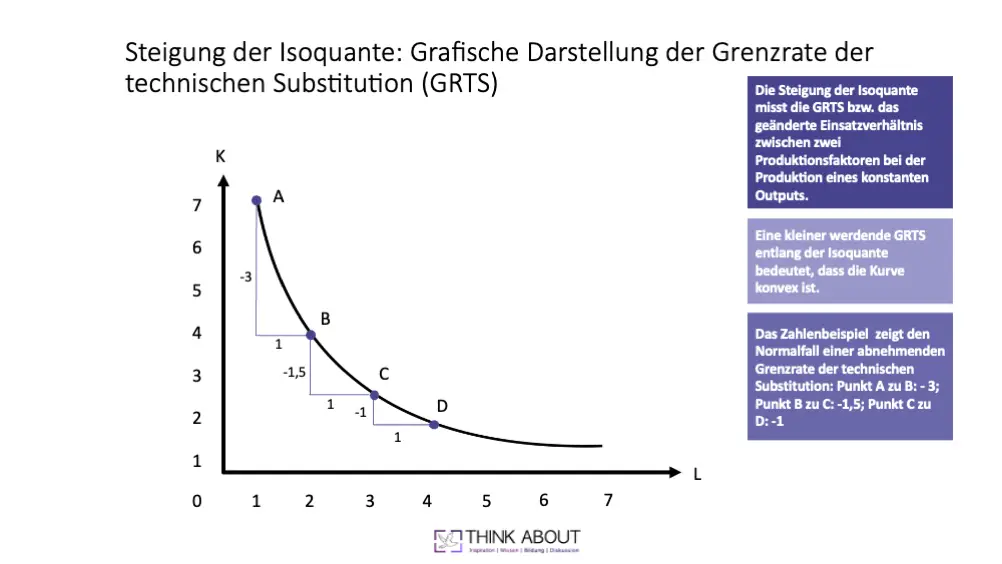
In der Grafik seht ihr für eine nicht näher spezifizierte Produktionsfunktion die Isoquante mit den Produktionsfaktoren Arbeit und Kapital und die sich ergebende Grenzrate der technischen Substitution.
Die Kurve weist einen fallenden Verlauf auf und über die Steigung könnt ihr die Grenzrate der technischen Substitution messen. In der Grafik ist dies beispielhaft mit vier Punkten dargestellt. Betrachtet ihr die Punkte A bis D seht ihr, dass die GRTS immer kleiner wird. Dies zeigt, dass die Isoquante konvex ist.
Ihr seht, dass es verschiedene Möglichkeiten gibt, die Grenzrate der technischen Substitution zu bestimmen. Ihr könnt sie einmal über die Produktionsfunktion berechnen. Oder, wie hier, wenn euch eine Kurve (mit Zahlen) gezeigt wird, über die Bewegung von einem Punkt auf der Kurve zu einem anderen Punkt ablesen.
Anwendungsgebiete der Grenzrate der technischen Substitution in der VWL
Hier sind einige Anwendungsgebiete der Grenzrate der technischen Substitution in Lehre und Praxis:
- Investitionsentscheidungen: Unternehmen können die GRTS verwenden, um zu entscheiden, welche Kombinationen von Produktionsfaktoren am effizientesten sind, um die gewünschte Produktionsmenge zu erreichen.
- Arbeitsmarkt und Lohnsetzung: Arbeitgeber können die GRTS verwenden, um zu entscheiden, wie viel sie für die verschiedenen Produktionsfaktoren bezahlen sollten, um die Produktionsmenge zu maximieren und gleichzeitig die Kosten zu minimieren.
- Handelspolitik: Die GRTS kann verwendet werden, um zu untersuchen, wie der Austausch von Gütern und Dienstleistungen zwischen Ländern beeinflusst wird, wenn unterschiedliche Faktorkombinationen und -kosten in den verschiedenen Ländern vorhanden sind.
- Umweltökonomie: Die GRTS kann verwendet werden, um zu untersuchen, wie die Verwendung von Ressourcen in der Produktion durch umweltfreundlichere Alternativen ersetzt werden kann, um den Ausstoß von Treibhausgasemissionen oder anderen schädlichen Umweltauswirkungen zu reduzieren.
- Innovationen: Die GRTS kann verwendet werden, um zu untersuchen, wie technologische Veränderungen die Effizienz der Produktion verbessern können, indem sie eine bessere Substitution zwischen den Produktionsfaktoren ermöglichen.
Insgesamt kann die GRTS helfen, die Produktion effizienter und kosteneffektiver zu gestalten und somit zur Verbesserung der Wirtschaftsleistung beitragen.
Von der VWL-Theorie in die Unternehmens-Praxis: Vor- und Nachteile der Grenzrate der technischen Substitution
Hier sind einige der wichtigsten Vor- und Nachteile:
