Isoquante erklärt: Definition, Berechnung, Grafik und Beispiele

Die Isoquante ist die grafische Darstellung einer Produktionsfunktion und gibt das Austauschverhältnis der eingesetzten Produktionsfaktoren an. In diesem Artikel erfahrt ihr, wie man die Isoquante zeichnet und berechnet. Außerdem stellen wir euch die wichtigsten Formen von Isoquanten vor.

Definition Isoquante einfach erklärt

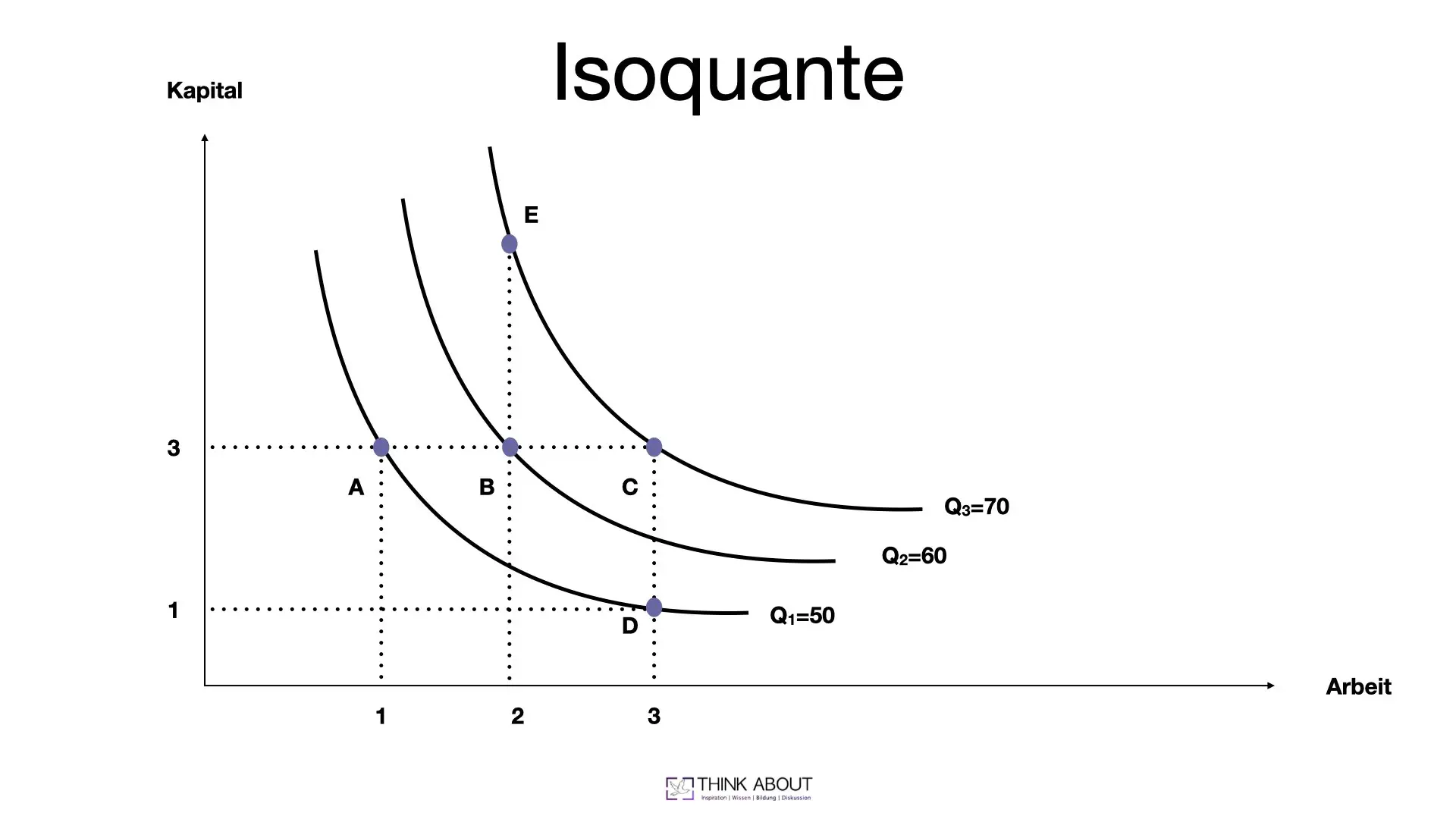
Die Menge eines Gutes, das ein Unternehmen produziert und auf dem Markt anbietet, hängt davon ab, wie hoch das erreichbare Outputniveau ist. In der Regel benötigt man die beiden Faktoren Kapitel und Arbeit zur Produktion des Gutes. Je nachdem, ob man eine kurzfristige oder langfristige Produktion betrachtet, sieht man den Faktor Kapitel als gegeben an. In der langfristigen Betrachtung ist er variabel.

Die Isoquante bildet die verschiedenen Kombinationsmöglichkeiten für eine bestimmte Produktionsmenge des Gutes ab.

Die Grafik zeigt nicht nur eine Isoquante, sondern eine Isoquantenschar. D. h. jede Isoquante bildet die Faktorkombinationen für eine andere Produktionsmenge ab.

Die Isoquante besitzt die folgenden Annahmen und Eigenschaften:

Hintergrund: Isoquante und Produktionsentscheidung

In der Mikroökonomie beschäftigt sich die Produktionstheorie mit den Entscheidungen von Unternehmen hinsichtlich ihrer Produktion. Sie gibt damit den Rahmen vor für die Angebotsseite des Marktes. Die zugehörigen Bestandteile des Modellrahmens, der zugehörigen Annahmen und Analysemethoden entsprechen in der Regel denjenigen aus der Haushaltstheorie. Die Haushaltstheorie untersucht das Entscheidungsverhalten der Haushalte bzw. Konsumenten, welche die Nachfrageseite des Marktgeschehens abbilden.

Eine Zielsetzung der Unternehmen ist es nun, ihr Angebot möglichst effizient zu produzieren und auf dem Markt anzubieten.

Das mikroökonomische Standardmodell zur Produktionsentscheidung geht von einem Unternehmen aus, das ein Gut produziert. Für die Herstellung dieses Gutes benötigt es zwei Produktionsfaktoren. Abhängig vom gewählten Lehrbuch lässt man diese Faktoren unbestimmt oder verwendet die Produktionsfaktoren Arbeit und Kapitel.

Wie nun das Gut produziert wird, bestimmt die Produktionsfunktion. Sie gibt an, welche Menge an Gütern bei einem bestimmten Einsatz der Produktionsfaktoren produziert, werden können. Allerdings existieren unendlich viele verschiedene Kombinationsmöglichkeiten der Produktionsfaktoren für die Produktion. Hier kommt jetzt die Isoquante ins Spiel: Sie zeigt grafisch, alle Kombinationsmöglichkeiten für ein bestimmtes Produktionsniveau an. 

Das Unternehmen muss jetzt aber noch entscheiden, welche Einsatzkombination der Produktionsfaktoren die effizienteste Produktion ermöglicht. Dies wird über die Zuhilfenahme der Isokostenlinie erreicht. Sie stellt die verschiedenen Faktorkombinationen dar, die das Unternehmen mit einem bestimmten Budget erreichen kann. Den Schnittpunkt der Isoquante und der Isokostenlinie bezeichnet man als Minimalkostenkombination. Hier befindet sich der Punkt, an dem das Unternehmen am effizientesten produziert.

Diesen Punkt strebt das Unternehmen bei seiner Produktionsentscheidung an.

Die Steigung der Isoquante: Grenzrate der technischen Substitution

Die Steigung der Isoquante ist die Grenzrate der technischen Substitution. Sie misst das Austauschverhältnis zweier Produktionsfaktoren.

Schau dir noch einmal die erste Grafik in diesem Artikel einer Isoquante an. Angenommen du befindest dich dort auf einem Punkt (K1, L1). Dann stellst du dir folgende Frage: Wie viel mehr vom Faktor L benötigst du, wenn du etwas vom Faktor K aufgibst? Dies ist dann die Steigung der Isoquante. 

Je nach Gestaltung der Produktionsfunktion bzw. in Abhängigkeit der für die Produktion vorliegenden Technologie kann die Steigung unterschiedlich ausfallen. In der Regel liegen sogenannte substitutionale Produktionsfunktionen vor. Das bedeutet, dass die Produktionsfaktoren gegeneinander ausgetauscht werden können. D.h. sie sind substituierbar. In diesem Fall weist die Isoquante eine negative Steigung, die auch effizient ist.

Vielleicht fällt dir beim Lesen wieder die Gemeinsamkeit mit den Indifferenzkurven und der Grenzrate der Substitution auf. Wir haben eingangs ja geschrieben, dass sich beide Analysekonzepte sehr ähnlich sind.

Es gibt aber dann doch einen entscheidenden Unterschied zwischen der Analyse der Haushalte und der Analyse der Unternehmen:

Der Unterschied besteht in der Messbarkeit einer Produktions- und einer Nutzenfunktion. Die Ausgestaltung und damit die Produktionsmöglichkeiten der Produktion sind von der eingesetzten Technologie abhängig. Die Menge der eingesetzten Produktionsfaktoren und der resultierende Output sind konkret messbar. Ihr erhaltet als Ergebnis des Prozesses konkrete Güter oder Dienstleistungen.

Nutzenfunktionen basieren u. a. auf Annahmen zu den Präferenzen der Konsumenten. Diese Präferenzen sind subjektiv. Entsprechend ist es schwierig, den Nutzen von Konsumenten infolge von Konsumentscheidungen zu messen. Man mildert diese Herausforderungen über Konzepte der kardinalen oder ordinalen Nutzenmessung ab.

Aber zusammengefasst besteht der Unterschied zwischen der Entscheidungsanalyse in der Messbarkeit des Outputs.

Zeichnen und Berechnung einer Isoquante

Du kannst die Isoquante berechnen und anschließend zeichnen, sofern du eine Produktionsfunktion vorliegen hast. Die Produktionsfunktion und die Steigung der resultierenden Isoquante, die Grenzrate der technischen Substitution, ist von der verwendeten Technologie der Produktionsfunktion abhängig. Die Technologie beeinflusst, ob bzw. wie das Einsatzverhältnis der Produktionsfaktoren ausgestaltet ist.

Im Folgenden zeigen wir dir drei Beispiele für Produktionsfunktionen und den hieraus resultierenden Isoquanten. Das „normale“ Beispiel ist eine substitutionale Produktionsfunktion, wofür wir eine Cobb-Douglas-Funktion nehmen. Dann zeigen wir dir noch die beiden Extrembeispiele für den Verlauf von Isoquanten: lineare Produktionsfunktionen und Minimum-Funktionen.

Der Ablauf für Berechnung und Zeichnung der Isoquante läuft aber immer in drei Schritten ab:

Isoquante und Produktionsfunktion 

1. Perfekte Substitute

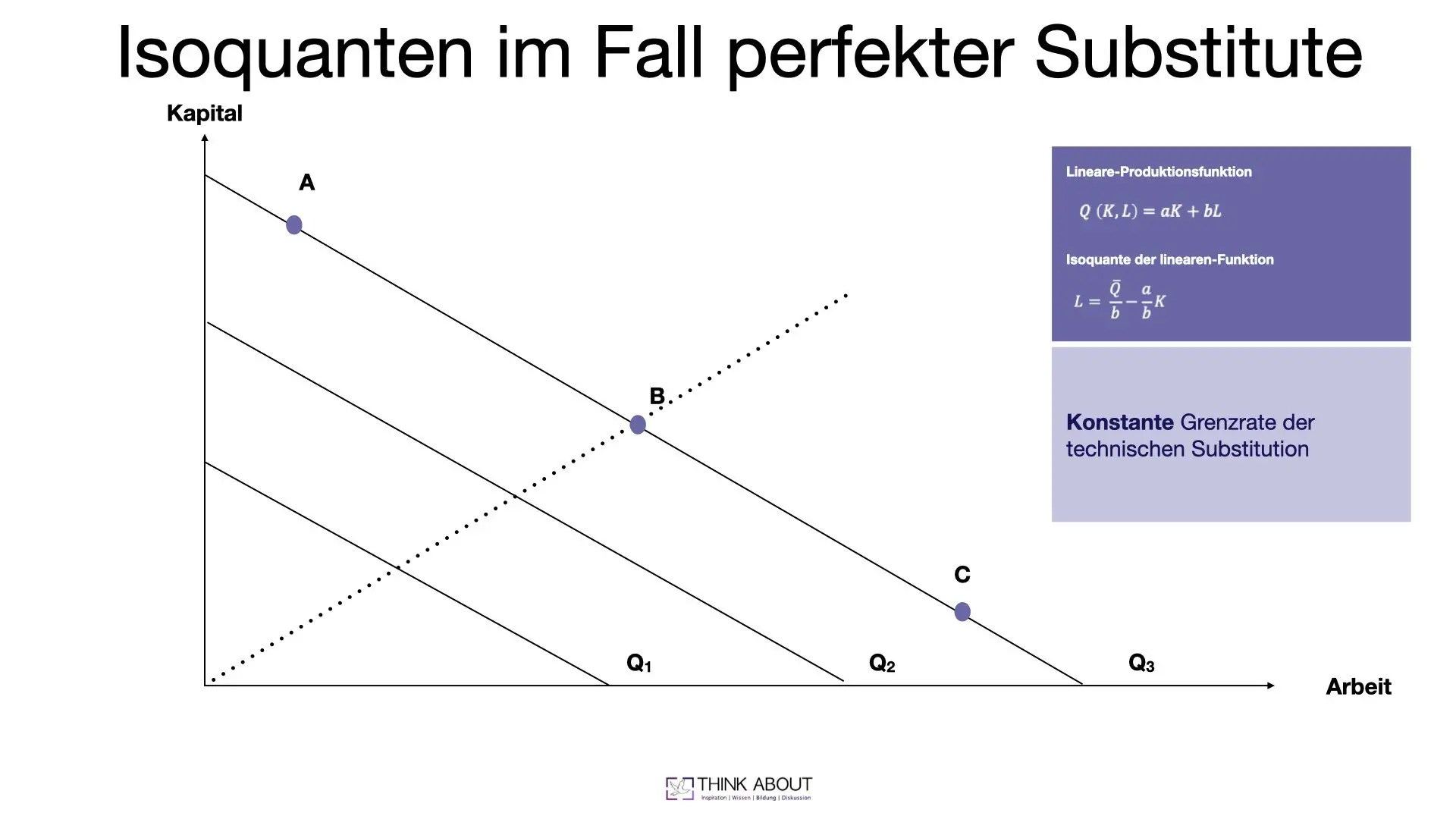
Das erste Beispiel für die Darstellung einer Isoquante ist eine Produktionsfunktion mit perfekten Substituten. In der Grafik sehr ihr die entsprechenden Isoquanten einer solchen Funktion. Wir haben dort als Produktionsfaktoren die Faktoren Arbeit und Kapital verwendet. Das Wichtigste, was ihr euch von diesem Beispiel mitnehmen solltet, ist, dass die Produktionsfaktoren vollständig miteinander austauschbar sind. Hieraus folgt, dass jeder Faktor für sich alleine dieselbe Outputmenge erzeugen kann.

Ein relativ intuitives Alltagsbeispiel wäre hierfür die Produktion von Hausaufgaben bzw. das Ausfüllen der Arbeitsblätter. Hierfür habt ihr rote und blaue Bleistifte zur Verfügung. Die verschiedenen Bleistifte sind eure Inputfaktoren. Es ist aber vollkommen egal, ob ihr die Arbeitsblätter mit dem blauen oder mit dem roten Bleistift ausfüllt. Ihr könnt nur mit einem einzigen Bleistifttyp dieselbe Menge an Output generieren.

Die zugehörige Produktionsfunktion ist eine lineare Produktionsfunktion:

Ihr seht, dass perfekte Substitute in diesem Fall immer additiv miteinander verbunden sind. Löst ihr die Gleichung beispielsweise nach dem Faktor Arbeit L auf, erhaltet ihr die zugehörige Isoquante:

Die Steigung der Isoquante ist das Austauschverhältnis der beiden Produktionsfaktoren. In diesem Beispiel dargestellt durch den Faktor -a/b. In der zugehörigen Grafik kannst du erkennen, dass der Output konstant bleibt, egal welchen Produktionsfaktor man mengenmäßig mehr verwendet. 

In der Haushaltstheorie gibt es bei den Indifferenzkurven den entsprechenden Typ. 

2. Perfekte Komplemente

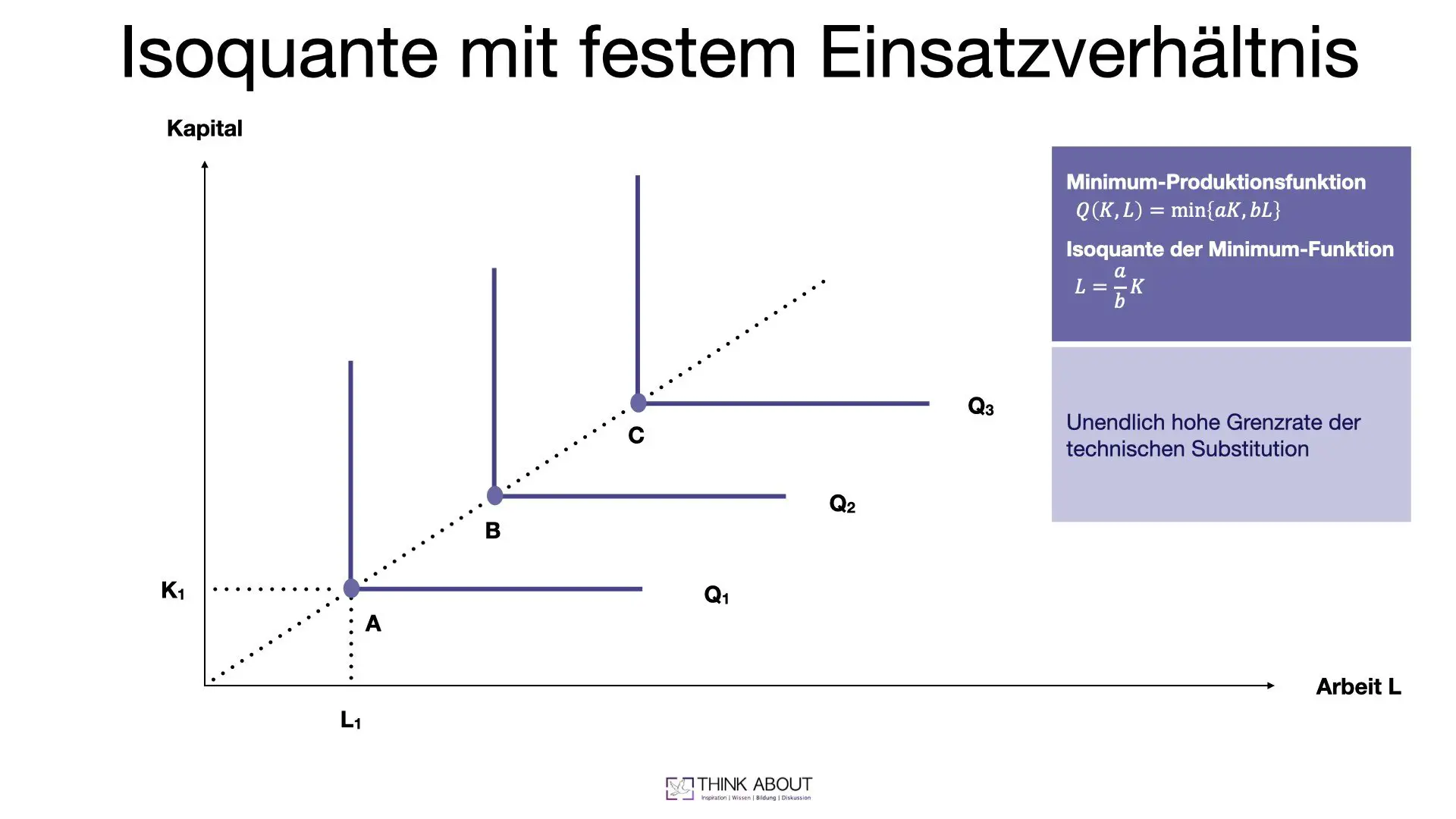
Unser zweites Beispiel ist eine Produktionsfunktion, deren Inputfaktoren perfekte Komplemente sind. Wie bei den perfekten Substituten handelt es sich hierbei eher um Ausnahmefälle, die Extrembeispiele für den Verlauf der zugehörigen Isoquanten darstellen. Das entsprechende Gegenstück findet man auch hier wieder in der Haushaltstheorie bei den Indifferenzkurven.

Die Produktionsfunktion lautet:

Es handelt sich hierbei um eine sogenannte Minimum-Funktion. Das Besondere an dieser Funktion ist, dass jeder Faktor ein Gegenstück, also ein Komplement, benötigt. Perfekte Komplemente bedeutet, dass sich die Inputfaktoren gegenseitig vervollständigen. Im Prinzip das Gegenteil von Substituten. Das Austauschverhältnis ist bei Komplementen deswegen immer konstant. Erhöhst du Faktor 1 um 2 Einheiten, musst du auch Faktor 2 um 2 Einheiten erhöhen, damit du deine Produktionsmenge erhöhen kannst.

Ein intuitives Alltagsbeispiel wäre die Gartenarbeit. Wenn du Löcher schaufeln möchtest, benötigst du Schaufeln und Menschen, die diese Schaufeln benutzen. Zusätzliche Schaufeln bringen dir überhaupt nichts, wenn du nicht noch weitere Helfer findest, die diese zusätzlichen Schaufeln benutzen. Die Gesamtzahl an Löcher, die gebuddelt werden können, bestimmen damit gemeinsam das Minimum der vorhandenen Schaufeln und das Minimum der anwesenden Helfer.

Die Isoquante ist damit nicht direkt berechenbar. Man stellt sie deshalb dar, in dem man die Inputfaktoren einfach miteinander kombiniert. Die resultierende Isoquante ist immer abhängig von der genauen Ausgestaltung der Produktionsfunktion. In unserem Beispiel haben wir:

Auf der punkteten Linie, bzw. in den Punkten, A, B und C weisen die beiden Produktionsfaktoren dieselbe Einsatzmenge auf. Weichst du von diesem Verhältnis ab, indem du einen Faktor erhöhst, bleibst du auf der Isoquante. Denn deine Produktionsmenge verändert sich nicht, da sie ja durch den kleineren Faktor bestimmt wird.

3. Imperfekte Substitute: Beispiel Cobb-Douglas-Funktion

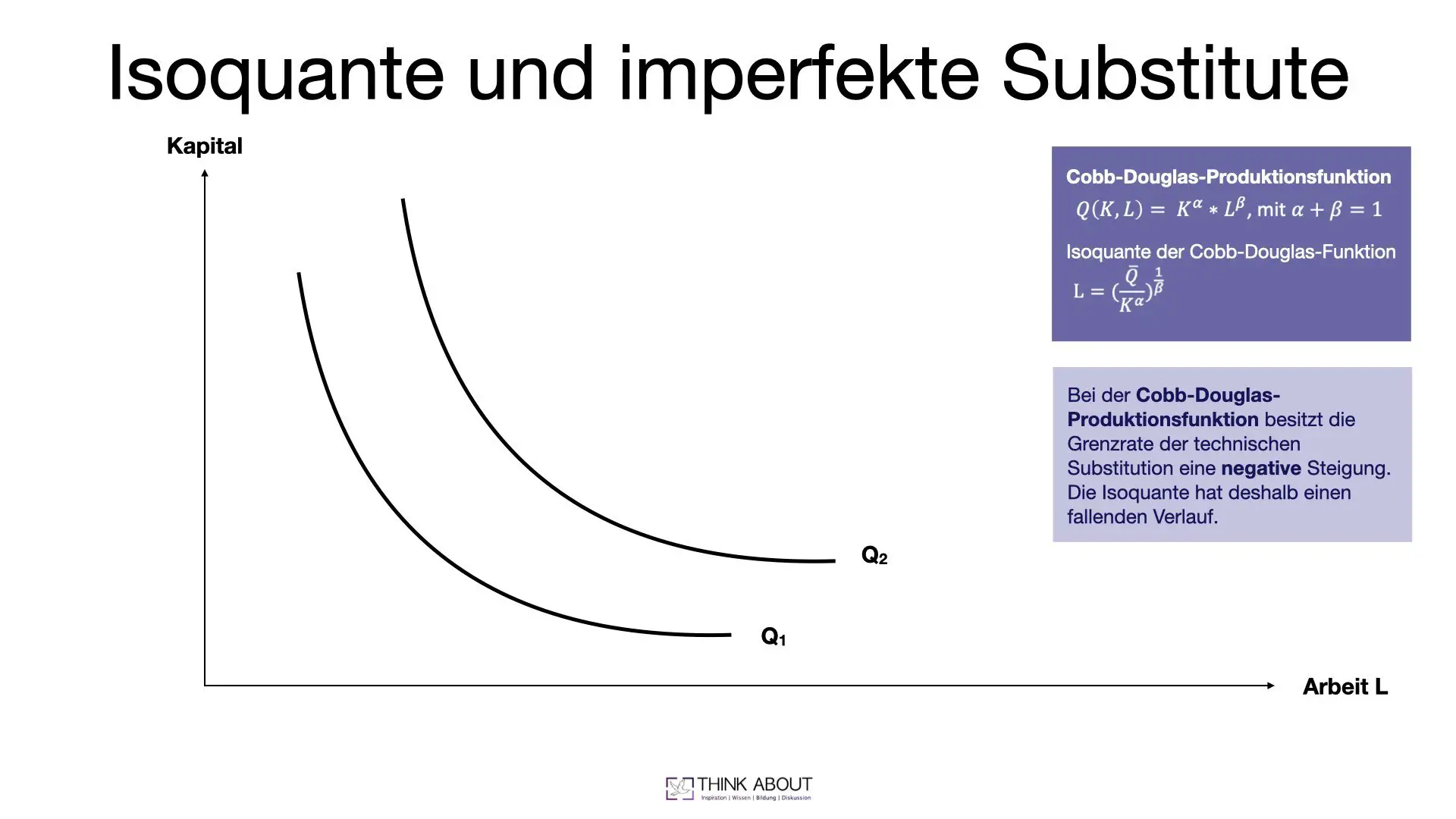
Hier siehst du am Beispiel einer Cobb-Douglas-Funktion die Darstellung einer Isoquante mit imperfekten Substituten. Wir haben wieder zur Veranschaulichung als Produktionsfaktoren die Faktoren Kapital und Arbeit verwendet. Imperfekte Substitute bedeuten, dass sich ein Produktionsfaktor nicht vollständig durch den anderen Faktor ersetzen lässt. D. h. egal wie stark man über Investitionen in Maschinen etc. den Faktor Arbeit verringert bzw. substituiert. Irgendjemand muss die Maschinen auch bedienen. Also wird der Faktor Arbeit niemals vollständig durch den Faktor Arbeit substituiert werden können.

Es gibt verschiedenste Möglichkeiten für die Ausgestaltung einer Produktionsfunktion mit imperfekten Substituten. Das gängigste Beispiel ist die Cobb-Douglas-Funktion. Ihr erkennt sie immer sofort daran, dass sich die Elastizitäten der Produktionsfunktion zu eins addieren.

Löst ihr die Funktion nach einem Faktor auf, könnt ihr hierüber die Isoquante grafisch darstellen. In der Grafik haben wir das für den Faktor L gemacht. Ihr seht, dass die Isoquante einen fallenden Verlauf hat. Die Grenzrate der technischen Substitution ist negativ.