Die Preiselastizität der Nachfrage ist ein Maß, um die Anfälligkeit der Nachfrage aus Preisänderungen zu messen. In diesem Artikel stellen wir euch Definition, Berechnungsmöglichkeiten und Interpretation dieser Elastizität vor.
Definition Preiselastizität der Nachfrage einfach erklärt
Preiselastizität der Nachfrage \epsilon_{p} : Maß für die Stärke, mit der die Nachfragemenge eines Gutes auf Änderungen seines Preises reagiert. Man berechnet sie als Quotient der prozentualen Änderung der Nachfragemenge zur prozentualen Änderung des Preises.
Die Definition für die Preiselastizität allgemein lautet:
Preiselastizität: Maß für die Stärke, mit der die Nachfragemenge oder die Angebotsmenge des Gutes auf eine Veränderung der Preise von Gütern auf dem Markt reagieren.
Diese allgemeine Definition der Preiselastizität berücksichtigt, dass es nicht nur eine direkte Preiselastizität der Nachfrage, sondern auch des Angebotes gibt. Zudem existieren auch indirekte Preiselastizitäten. Hierzu ist die Substitutionselastizität zu nennen.
Die wichtigste und bekannteste Elastizität ist aber die Preiselastizität der Nachfrage. Umgangssprachlich bezeichnet man sie deshalb auch als Preiselastizität oder Nachfrageelastizität.
Verschiedene Elastizitäten: Elastizität, Preiselastizitäten und Einkommenselastizität
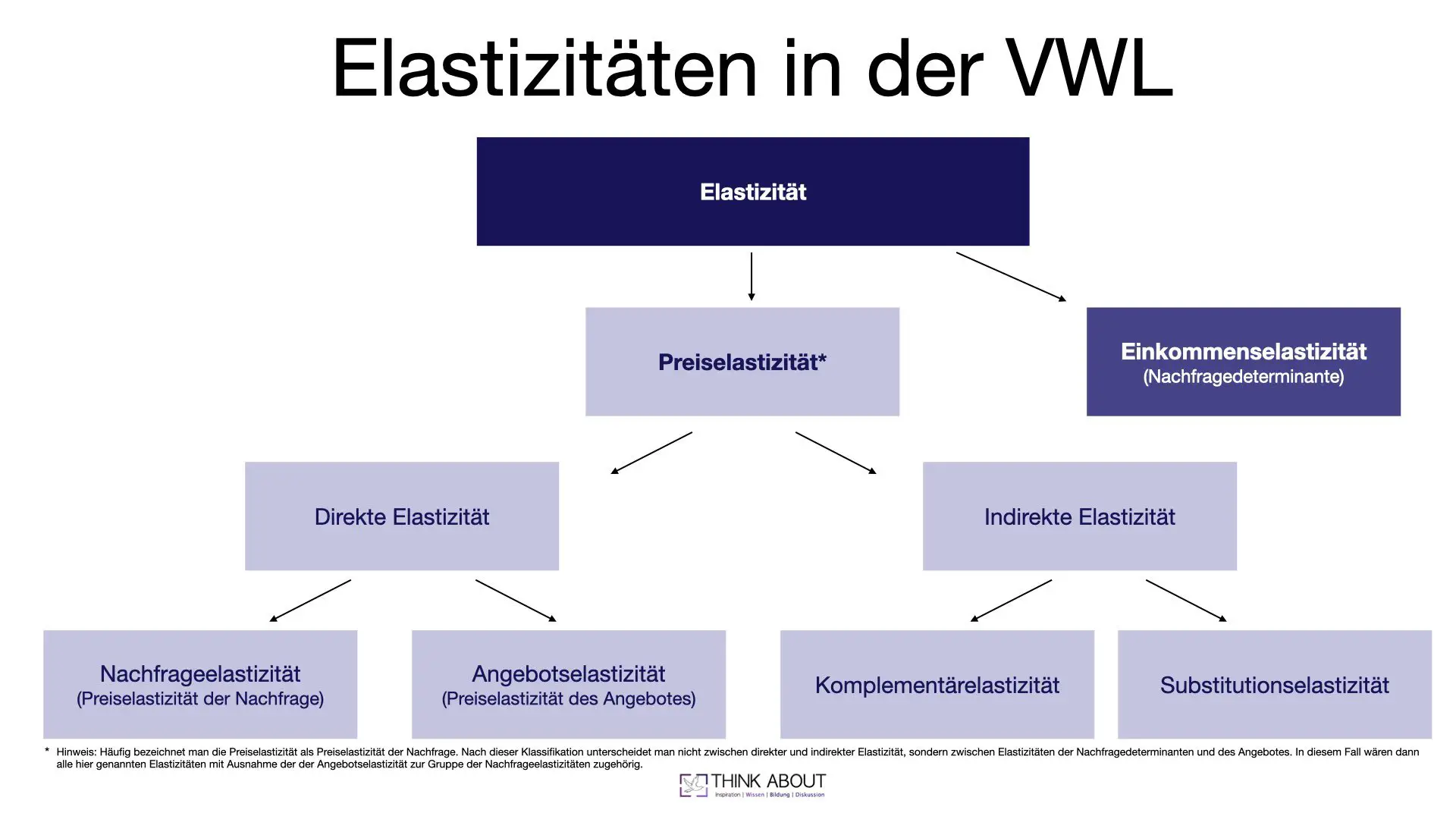
In dieser Grafik seht ihr, was wir bereits im Abschnitt zur Definition angesprochen haben. In der VWL existieren verschiedenste Elastizitäten, die Reaktionen auf unterschiedliche Marktdeterminanten messen.
Zum einen kann man zwischen der Preiselastizität und der Einkommenselastizität unterscheiden. Erstere misst die Reaktionsstärke auf Preisänderungen.
Die Einkommenselastizität misst dagegen, wie stark sich eine Änderung des Einkommens der Haushalte auf die Nachfragemenge auswirkt. In der Haushaltstheorie der Mikroökonomie ist neben dem Güterpreis das Haushaltseinkommen eine Nachfragedeterminante und damit Bestandteil des Optimierungsproblems, wie er bei gegebenen Determinanten (Einkommen, Preise) seinen Nutzen maximieren kann.
In Abhängigkeit davon, welche Preisänderungen man untersucht, unterscheidet man zwischen einer direkten Preiselastizität und der indirekten Preiselastizität.
Die direkte Preiselastizität misst, wie stark sich die Änderung des Preises eines Gutes auf die Marktmenge auswirkt. Je nachdem, ob man des Preises auf der Nachfrage- oder Angebotsseite darstellt, unterscheidet man zwischen der Angebotselastizität bzw. der Preiselastizität des Angebotes. Und der Nachfrageelastizität bzw. der Preiselastizität der Nachfrage.
Die indirekte Preiselastizität, auch Kreuzpreiselastizität genannt, misst dagegen, wie stark sich die Nachfragemenge eines Gutes ändert, wenn sich der Preis eines verwandten Gutes ändert. Je nachdem, ob es sich bei dem Gut, um ein Substitut oder ein komplementäres Gut handelt, bezeichnet man die resultierende Elastizität dann als Substitutionselastizität oder Komplementärelastizität.
Von der Bedeutung der aufgeführten Elastizitäten, ist die Preiselastizität (der Nachfrage) mit Abstand die bedeutendste. Je nach Lehrbuch oder Literaturquelle kann sich die Klassifikation der Elastizitäten und damit auch die Bezeichnung der Preiselastizität unterscheiden. Eine weitere Möglichkeit ist es, zwischen Marktseiten zu unterscheiden. D. h. man würde die Einkommenselastizität als Nachfragedeterminante betrachten und damit zur Gruppe der Nachfrageelastizitäten zählen. Dem Gegenüber würde dann die Angebotselastizität separat betrachtet werden.
Formel und Berechnung der Preiselastizität der Nachfrage
Hier seht ihr die einfachste Formel zur Berechnung der Preiselastizität der Nachfrage \epsilon_{p} . Es gilt:
\epsilon_{p} = Prozentuale \: Änderung \: der \: Nachfragemenge / Prozentuale \: Preisänderung = (\Delta Q_{D})/(\Delta p)
wobei:
\epsilon_{p} = Betrag der Elastizität
p = Preis des Gutes
Q = nachgefragte Menge des Gutes. Wir haben in der Formel das Q deshalb noch mit einem kleinen D gekennzeichnet. Im Falle der Angebotselastizität wäre Qs die angebotene Menge des Gutes
Die hier verwendeten Buchstaben für die Bezeichnungen variieren in der Literatur. Manchmal nimmt man für die Menge anstelle von Q den Buchstaben x. Oder für die Elastizität nimmt man einen anderen griechischen Buchstaben.
Mit der obigen Formel kann man die Elastizität ganz einfach berechnen. Konfrontiert man euch beispielsweise mit der Aussage, dass der Preis für Bier um 10 % gestiegen ist, und daraufhin die Nachfrage nach Bier um 20 % gesunken ist, setzt ihr die beiden Prozentwerte einfach in die Formel und erhaltet die zugehörige Preiselastizität der Nachfrage: -20 %/10 % = I -2 I = 2.
Man berechnet die Elastizität über Prozentwerte, damit man keine Interpretationsprobleme über uneinheitliche Maße bekommt. Beispielsweise, wenn man Elastizitäten für Güter in verschiedenen Ländern mit unterschiedlichen Währungen berechnet, kann es sonst zu Interpretationsproblemen kommen.
Ausgehend von der obigen Formel kann man die Elastizität der Nachfrage noch über andere Formeln berechnen, die insbesondere aus dem Zusammenhang zwischen der Steigung der Nachfragekurve und der Preiselastizität resultieren.
Die beiden wichtigsten Berechnungsformen lauten:
1. Punktelastizität der Nachfrage
\epsilon_{p} =\left| \frac{\partial Q}{\partial p} \ \times \ \frac{p}{Q} \right|
= |(Q_{2}-Q_{1})/(p-p_{1})*p_{1}/Q_{1}|
Man gelangt über einige mathematische Umformungen von der obigen Formel zu dieser Formel, wenn man beachtet, dass \frac{\Delta Q}{\Delta p} =\frac{\partial Q}{\partial p} =\frac{1}{\frac{\partial p}{\partial Q} } .
Etwas vereinfacht formuliert, stellt die Preiselastizität den Kehrwert der Steigung der Nachfragekurve dar, bezogen auf einen bestimmten Punkt, um die prozentuale Veränderung zu berechnen. Hierbei nimmt man dann den Ausgangspunkt 1.
Das Problem bei dieser Formel ist allerdings, dass die resultierende Punktelastizität schwankt, da sie vom Ausgangswert abhängt. So ist eine Preissteigerung von 4 auf 5 Euro ein Anstieg von 25 %. Eine Preissenkung von 5 auf 4 Euro ist dagegen ein Rückgang von 20 %. Entsprechend ergeben sich verschiedene Werte für die jeweils resultierende Punktelastizität.
Um dieses Problem zu beheben, berechnet man die sogenannte Bogenelastizität nach der Mittelwertmethode.
2. Bogenelastizität
\epsilon_{p} =(Q_{2}-Q_{1})/[(Q_{2}+Q_{1})/2]/(p_{2}-p_{1})/[(p_{2}+p_{1})/2]
Der Unterschied zwischen den beiden Formeln besteht im Umgang mit dem Ausgangspunkt, der im zweiten Teil der Gleichung steht. Bei der Mittelwertmethode nutzt man keinen einzelnen Punkt, sondern nutzt den Mittelwert aus dem Ausgangs- und Endpunkt.
Bezogen auf unser vorheriges Beispiel ist der Mittelwert der beiden Preise von 4 und 5 Euro 4,5 Euro. Einen entsprechenden Mittelwert berechnet man für die zugehörige Nachfragemenge. Die resultierende Preiselastizität wäre dann unabhängig davon, ob man eine Preiserhöhung oder Preissenkung betrachtet, immer dieselbe Elastizität ergeben.
Interpretation, Bedeutung der Preiselastizität der Nachfrage und die Nachfragekurve
Für die Interpretation der Preiselastizität betrachtet man den Betrag. D. h., auch wenn man bei einer Nachfragekurve eine negative Steigung und damit auch eine negative Elastizität hat, betrachtet man nur den Wert. Also beispielsweise nicht – 2, sondern 2. Man interpretiert damit immer positive Elastizitäten, selbst wenn sie rechnerisch negativ sind. Man unterscheidet generell zwischen einer preiselastischen und einer preisunelastischen Nachfrage.
Es gilt:
\epsilon_{p} < 1: Preisunelastische Nachfrage
\epsilon_{p} > 1: Preiselastische Nachfrage
Eine preiselastische Nachfrage bedeutet, dass die prozentuale Änderung der nachgefragten Menge größer ausfällt als die prozentuale Änderung des Preises. Bei einer preisunelastischen Nachfrage fällt die prozentuale Änderung der nachgefragten Menge entsprechen kleiner aus als die prozentuale Änderung des Preises.
Die nachfolgende Grafik stellt den Zusammenhang zwischen einer linearen Nachfragekurve und der Preiselastizität der Nachfrage dar.

Wir möchten euch darauf hinweisen, dass wir der Einfachheit halber immer von linearen Kurven oder Funktionen sprechen. Die Nachfragekurve muss aber nicht linear sein. Sie kann auch gekrümmt sein. Die Form hat Auswirkungen auf die Steigung. Bei einer linearen Kurve ist die Steigung immer konstant, da sie das Verhältnis aus zwei Punkten misst. Die Elastizität der verschiedenen Punkte auf der Kurve fällt dagegen unterschiedlich aus, da hier das Verhältnis der Veränderungen von Punkten gemessen wird.
Hieraus folgt, dass -wie in der Grafik dargestellt-, sich entlang der Nachfragekurve die Elastizität ändert. Und man die Nachfragekurve in einen elastischen und in einen unelastischen Bereich gliedern kann. Deshalb berechnet man neben der Punktelastizität auch die Bogenelastizität, um diese Unterschiede auszugleichen.
Die unterschiedliche Elastizität entlang der Nachfragekurve besitzt außerdem eine hohe Bedeutung für die Absatzplanung der Unternehmen. Denn die inverse Nachfragekurve ist die Preis-Absatz-Kurve der Unternehmen. Oder anders formuliert: Die nachgefragte Menge entspricht dem Absatz des Unternehmens und hat gemeinsam mit der Preishöhe eine große Bedeutung für den erzielbaren Erlös (Erlös = Preis * abgesetzte Menge).
Preiselastizität der Nachfrage, Nachfragekurve und Umsatz der Unternehmen
Beispielrechnung Preiselastizität und Nachfragekurve
Die Tabelle baut auf der Grafik und Erklärung zum Zusammenhang zwischen Preiselastizität und Nachfragekurve, so dem möglichen Erlös von Unternehmen auf.
Für ein nicht näher bestimmtes Gut seht ihr in den ersten beiden Spalten die Preise und die dazugehörige nachgefragte Menge.
Auf Basis dieser Informationen sind in den übrigen Spalten der Erlös, Preis- und Mengenänderungen in %, sowie die Punktelastizität und die hieraus jeweils resultierende Bogenelastizität (Mittelwert aus zwei Punkten) berechnet wurden. Die Elastizitäten, die größer 1 sind, bilden eine elastische Nachfrage auf Preisänderungen. Werte < 1, sind unelastisch.
Ihr seht, dass es einen Punkt gibt, an dem die Elastizität \epsilon_{p} = 1 ist. An diesem Punkt erzielt das Unternehmen seinen höchsten Erlös mit 24,5 Euro. Hier liegt sein Gewinnoptimum. Stellt ihr euch zudem die Werte der Erlöse bildlich als Kurve vor, erkennt ihr, dass die „Erlöskurve“, wie eine Glocke geformt ist. Im unelastischen Bereich der Nachfragekurve steigt der Erlös. Solange, bis das Optimum erreicht ist. Anschließend sinkt der Erlös wieder und damit auch die Erlöskurve. Hier liegt der elastische Bereich der Nachfragekurve.
Knapp formuliert bedeutet diese Beobachtung, dass wir zwei Effekte betrachten müssen. Die Höhe des Gesamteffektes ist dabei abhängig von der Preiselastizität. Bei diesen zwei Effekten handelt es sich um den direkten Preiseffekt infolge einer Preisänderung und dem dazugehörigen indirekten Mengeneffekt. Die Höhe des Gesamteffektes ist davon abhängig, welcher Effekt stärker ausfällt.
Preiselastizität \epsilon_{p} < 1: Unelastische Nachfrage. Kaum Änderungen bei der nachgefragten Menge infolge von Preisänderungen. Preiseffekt > Mengeneffekt, Erlös steigt bei Preissteigerung.
Preiselastizität \epsilon_{p} > 1: Elastische Nachfrage. Starke Änderung bei der nachgefragten Menge infolge von Preisänderungen. Preiseffekt < Mengeneffekt, Erlös sinkt bei Preissteigerung.
Beispiele zur Berechnung der Preiselastizität der Nachfrage
1. Prozentwerte
Angenommen, der Verband der Eisdielenbesitzer überlegt in Hinblick auf den kommenden Sommer, die Preise für eine Kugel Eis zu erhöhen, um die gestiegenen Kosten in der Produktion decken zu können. Zur Entscheidungsfindung möchte er die Preiselastizität nutzen. Bevor weitere Informationen zum Absatz gesucht werden, soll einmal grob auf Basis von Erfahrungswerten der letzten Jahre überschlagen werden. Wie lautet die Preiselastizität, wenn bei einer Preiserhöhung von 4 % die Nachfrage um 2 % abnimmt?
Ihr setzt die beiden Werte in die allgemeine Formel der Preiselastizität ein:
\epsilon_{p} =\left| \frac{-2\ \% }{4\ \% } \right| =0,5
Die Elastizität \epsilon_{p} ist kleiner 1. Die Nachfrage nach Eiscreme ist damit relativ unelastisch.
2. Punktelastizität der Nachfrage
Jetzt möchte der Eisdielenverband die Preiselastizität etwas ausführlicher berechnet bekommen. Sie haben in ihren Unterlagen nachgeschaut und die alten Absatzmengen für Eiscreme mit den zugehörigen Preisen herausgesucht. Dabei haben sie gesehen, dass sie bereits vor zwei Jahren eine Preiserhöhung gehabt haben.
Damals betrug der Preis je Kugel 1 €. Nach der Preiserhöhung 1,5 €. Vor der Preiserhöhung haben sie 1000 Kugeln Eis verkauft, nach der Preiserhöhung nur noch 800 Kugeln Eis.
Wie lautet anhand dieser Vorgaben die Preiselastizität?
Ihr setzt die Werte in die Formel der Punktelastizität ein und löst auf:
(800 - 1.000) / (1,5 - 1) × 1/1000 = -200 / 0,5 × 1 /1.000 = 0,4
Die Punktelastizität beträgt 0,4. Das Ergebnis ist ähnlich, zu der vorherigen Berechnung. Sie zeigt aber, dass die Nachfrage in diesem Punkt sogar noch unelastischer war.
3. Beispiel Nachfragefunktion und Preiselastizität
Aufgrund der engen Beziehung zwischen Preiselastizität und Nachfragekurve könnt ihr die Preiselastizität der Nachfrage auch über die Nachfragefunktion berechnen. Hierfür müsst ihr die Funktion ableiten und dann die gegebenen Werte einsetzen.
Eine weitere Gleichung der direkten Preiselastizität der Nachfrage in Bezug auf die Nachfragekurve lautet:
\epsilon_{p} =|Q(p)*p/(Q(p))|
Bei dem ersten Term der Gleichung handelt es sich um die Ableitung der Nachfragefunktion. Der zweite Teil ist der Preis, geteilt durch die Nachfragefunktion.
Nehmen wir jetzt in einem anderen Beispiel an, ihr habt eine Nachfragefunktion Q(p) = 400 – 50p vorliegen und sollt die Punktelastizität für den Preis von 5 Euro berechnen.
Hierfür leitet ihr zuerst die Nachfragefunktion ab:
Q´(p) = – 50
Q(p) = 400 – 50p
Dann setzt ihr die Funktionen und Werte des Preises =5 in die Gleichung ein und löst auf:
\epsilon_{5} = I (- 50) × p / 400 – 50p I= I(-50)* 5 /(400 – (50 × 5))I = I- 250 / 150I = 1,67
Aufgrund der Betragsstriche gibt man den positiven Wert als Ergebnis an.
Einflussgrößen der Preiselastizität der Nachfrage
Verfügbarkeit substitutiver Güter
Substitute weisen eine hohe Preiselastizität der Nachfrage auf. Je einfacher es für die Konsumenten ist, ein verwandtes Gut als Ersatz zu finden, desto schneller bzw. stärker reagieren sie auf Preisänderungen mit einem Anstieg oder einem Rückgang ihrer Nachfrage nach diesem Gut. Ein gängiges Beispiel ist der Konsum von Butter und Margarine. Die beiden Güter sind sich sehr ähnlich. Eine Preiserhöhung von Butter führt entsprechend dazu, dass Konsumenten einfach auf Margarine ausweichen können.
Hieraus folgt, dass je näher sich zwei Güter in ihren Eigenschaften sind, desto höher ist die Preiselastizität der Nachfrage für das betrachtete Gut.
Ein extremes Gegenbeispiel wäre der Vergleich von Butter und Eiern. Beide Güter können nicht gegeneinander ausgetauscht werden. Vielmehr handelt sich um Komplementärgüter, wenn man z. B. Kuchen backen möchte. Entsprechend werden Butter und Eier eine sehr geringe Preiselastizität zueinander aufweisen.
Notwendige Güter versus Luxusgüter
Es bedarf eigentlich keiner großen Begründung, dass Güter des Alltags zur Befriedigung der Grundbedürfnisse eine relativ unelastische Nachfrage in Bezug auf Preisänderungen aufweisen. Hierzu zählen z. B. die Miete von Mietwohnungen, oder Gas und Strom. Steigen die Preise von Gas oder Strom, können die Menschen zwar in gewissen Umfang ihren Verbrauch senken. Aber ein mehr oder weniger hoher Grundbedarf bleibt bestehen. Entsprechend unelastisch ist die Nachfrage.
Güter, die dagegen nicht für den alltäglichen Grundbedarf notwendig sind, weisen eine hohe Preiselastizität auf. Solche Güter bezeichnet man oft als Luxusgüter. Nehmen wir beispielsweise die Anschaffung eines Tablets von Apple. Abgesehen von der Notwendigkeit in Schule, Studium etc. mit modernen Technologien arbeiten zu können, ist der Erwerb eines Tablets von Apple ein Luxusgut. Bei einer entsprechenden Preiserhöhung dürfte die Nachfrage deutlich zurückgehen. Apple-Sympathisanten werden mir an dieser Stelle wahrscheinlich sehr deutlich widersprechen. Für sie ist das Apple Tablet kein Luxusgut, sondern ein normales Gut.
Entsprechend ist es wichtig sich zu merken, dass ein bei der Einteilung eines Gutes in „normal“ oder „Luxus“ mit der entsprechenden Preiselastizität der Nachfrage nicht auf die Klassifikation des Gutes ankommt. Vielmehr ist der betrachtete Fall entscheidend. Wie definiert der Konsument das Gut? Wie stark sind seine Präferenzen für genau dieses Gut, diese Marke etc.? Entsprechend ändert sich auch die Elastizität.
Marktabgrenzung
Wann ein Gut leicht zu ersetzen ist, hängt auch davon ab, wie der entsprechende Markt definiert und abgegrenzt ist. Die Preiselastizität der Nachfrage dürfte für entsprechend definierter Märkte und Güter recht elastisch sein, da Nachfrager hier recht einfach auf entsprechende Alternativen ausweichen können. Betrachtete man z.B. die recht breite Kategorie Nahrungsmittel, dürfte die Nachfrageelastizität recht unelastisch sein. Denn womit soll man Nahrungsmittel bei Preiserhöhungen ersetzen? Schaut man sich dagegen das Gut Vollkornbrot als Teilmenge an, ist hier eine elastische Nachfrage zu erwarten. Denn je nach Präferenz können Konsumenten bei Preiserhöhungen leicht auf andere Brotsorten ausweichen.
Anteil des Einkommens für Konsumausgaben
Ähnlich zur Begründung der Preiselastizität für normale versus Luxusgüter spielt bei der Bedeutung des Anteils des Einkommens eine Rolle, ob es sich bei den betrachteten Gütern um normale oder sogenannte inferiore Güter handelt. Die Logik ist ähnlich, nur wird jetzt das Einkommen betrachtet. So weisen Konsumgüter, wie z. B. Lebensmittel in der Regel nur einen geringen Preis aus. D. h. für diese Güter gibt man nur einen relativ geringen Anteil seines Einkommens aus. Höherwertige und eher langfristig anzuschaffende Güter, wie z. B. Möbel, weisen dagegen in Relation hohe Preise aus. Für diese Güter gibt man entsprechend, einen relativ hohen Anteil seines Einkommens aus. Steigen beispielsweise die Preise von Möbeln um 10 % hat diese Preissteigerung absolut gesehen eine größere Auswirkung auf unser verfügbares Einkommen, als wenn die Preise der Lebensmittel um 10 % steigen würden. Auf den Kauf der Möbel wird man deshalb eher verzichten. Allgemein kann man schlussfolgern, dass die Elastizität der Nachfrage für ein Gut umso höher ist, je mehr man relativ gesehen von seinem Einkommen für dieses Gut ausgeben muss.
Zeithorizont
Auf lange Sicht ist die Preiselastizität der Nachfrage eines Gutes höher als kurzfristig. Der Grund ist ähnlich, wie die hohe Preiselastizität bei substitutiven Gütern. Nehmen wir als Beispiel die Nachfrage nach Benzin. Kurzfristig würde ein Preisanstieg von Benzin nur zu einem geringen Nachfragerückgang führen. Solange die Menschen in ihrer Mobilität auf ihr Auto mit dem entsprechenden Benzinbedarf angewiesen sind, kann die Nachfrage auch nicht entsprechend auf Preisänderungen reagieren. Erst langfristig, wenn beispielsweise Alternativen über einen Ausbau und eine preiswerte Nutzung des öffentlichen Nahverkehrs oder treibstoffsparende Autos geschaffen wurden, dürfte sich auf eine Preiserhöhung ein deutlicherer Preisrückgang ergeben.
Empirie: Vorgehen und Probleme bei der Schätzung der Preiselastizität
Wie berechnet man die Preiselastizität der Nachfrage in der Praxis? Aufgrund der vorgestellten Rechenbeispiele könnte man denken, dass es einfach ist, die Elastizität zu berechnen. Man könnte auf die Seite des Statistischen Bundesamtes gehen und für ein bestimmtes Gut oder eine Gütergruppe Daten für die Nachfrage und die Preisentwicklung anschauen. Zwei dieser Werte gibt man dann in die entsprechende Formel ein und man hat die Preiselastizität berechnet.
Leider ist es in der Praxis dann doch nicht so einfach. Die Preiselastizität ist zwar eng verbunden mit der Nachfrage, aber der Preis ist nun einmal nicht der einzige Faktor, der das Nachfrageverhalten der Konsumenten beeinflusst. Die auffälligsten Faktoren wären z. B. das Einkommen und Preise verwandter Güter. Und da die nachgefragte Menge spiegelbildlich der angebotenen Menge der Unternehmen entspricht, ist es darüber hinaus teilweise schwierig eindeutig zwischen Faktoren zu trennen, die nur das Angebot oder nur die Nachfrage beeinflussen.
Zur Schätzung der Preiselastizität verwenden Volkswirte deshalb statistische Analyseverfahren, in der Regel Regressionsverfahren. Es existiert ein breites und umfangreiches Forschungsgebiet, welches sich mit der Schätzung von Elastizitäten und allgemeiner der korrekten Einflussparameter der Nachfrage und des Angebotes beschäftigt.
Aufgrund der teils unterschiedlichen zugrundeliegenden Daten und Abweichungen in den Schätzmethoden oder ergänzenden Variablen zur Berücksichtigung relevanter ergänzender Faktoren unterscheiden sich die berechneten Elastizitäten über die Studien. Allerdings sind in der Regel ähnliche Trends oder auch ähnliche Werte zu beobachten. So, dass im Laufe der Zeit auf, die oben genannten „Gesetzmäßigkeiten“ geschlossen wurde, wann welche Güter elastisch oder unelastisch auf Preisänderungen reagieren.
Zusammengefasst, ist es in Bezug auf die Schätzung der Preiselastizität wichtig zu wissen, dass man für eine korrekte Berechnung mehr als zwei Parameter (Menge und Preis) benötigt. Solche „deskriptiv“ berechneten Elastizitäten mittels der Formel bilden aber einen guten Ausgangspunkt, um sich einen ersten Eindruck über die Elastizität des interessierenden Gutes zu machen.



