Die Grenzrate der Substitution misst das Verhältnis, bei dem ein Individuum gerade bereit ist, auf ein Gut zu verzichten, um von einem anderen Gut mehr zu erhalten. In diesem Artikel erklären wir Definition, Interpretation und Berechnung der Grenzrate der Substitution. Außerdem gehen wir auf ihre Bedeutung in der Haushaltstheorie ein, sowie auf Herausforderungen bei der Berechnung in der Praxis.
Definition Grenzrate der Substitution einfach erklärt
Die Grenzrate der Substitution (GRS) gibt an, wie viel von einem Gut ein Individuum bereit ist aufzugeben, um eine zusätzliche Einheit eines anderen Gutes zu erhalten, bei gleichbleibendem Nutzen. Sie ist also das Verhältnis der Grenznutzen der beiden Güter.
Bei der Grenzrate der Substitution handelt es sich um die Steigung der Indifferenzkurve. Man kürzt sie oft als „GRS“ oder „MU“ (marginal utility = Grenznutzen) ab.
Formel der Grenzrate der Substitution
Die Formel für die Grenzrate der Substitution (GRS) lautet:
GRS = - \frac{MU_{1}}{MU_{2}}
wobei MU1 der Grenznutzen des Gutes 1 und MU2 der Grenznutzen des Gutes 2 ist. Das negative Vorzeichen zeigt an, dass die GRS abnimmt, wenn der Konsum von Gut 2 zunimmt, wenn der Nutzen konstant bleibt.
Wie interpretiert man die Grenzrate der Substitution?

Die GRS gibt an, wie leicht ein Individuum bereit ist, ein Gut gegen ein anderes auszutauschen, um den gleichen Nutzen zu erhalten.
1. Eine höhere GRS bedeutet, dass das Individuum leichter bereit ist, ein Gut gegen ein anderes auszutauschen.
2. Eine niedrigere GRS bedeutet, dass es schwerer ist, ein Gut gegen ein anderes auszutauschen.
Wirtschaftshistorischer Hintergrund
Die Grenzrate der Substitution (GRS) wurde von dem österreichischen Ökonomen Eugen von Böhm-Bawerk entwickelt. Böhm-Bawerk war einer der bedeutendsten Vertreter der österreichischen Schule der Nationalökonomie und trug maßgeblich zur Entwicklung der neoklassischen Mikroökonomie bei.
Er prägte den Begriff "Grenznutzentheorie" und führte den Begriff der „GRS“ in seinem Werk "Grundzüge der Theorie des wirtschaftlichen Güterwerts" (1884) ein. Die GRS ist seitdem zu einem wichtigen Konzept in der Mikroökonomie geworden, dass in verschiedenen Bereichen der Wirtschaftsanalyse und Entscheidungsfindung Anwendung findet.
Bedeutung der Grenzrate der Substitution in der Haushaltstheorie
In der Haushaltstheorie spielt die Grenzrate der Substitution (GRS) eine zentrale Rolle. Die Haushaltstheorie beschäftigt sich mit der Entscheidungsfindung von Individuen oder Haushalten in Bezug auf den Konsum von Gütern und Dienstleistungen.
Die GRS ist dabei ein Maß dafür, wie viel von einem Gut durch ein anderes ersetzt werden kann, während der Nutzen konstant bleibt. Es beschreibt somit, wie viel ein Individuum bereit ist, von einem Gut aufzugeben, um eine zusätzliche Einheit eines anderen Gutes zu erhalten.
Die Haushaltstheorie nutzt die GRS, um die Entscheidungen von Individuen bei der Wahl von Konsummöglichkeiten zu erklären. Individuen wählen dabei in der Regel eine Kombination von Gütern, die ihren Präferenzen entspricht und die mit ihrem Budget vereinbar ist. Durch die GRS wird berechnet, welche Güterkombinationen für das Individuum am vorteilhaftesten sind und welche Veränderungen im Preisverhältnis der Güter zu einer Substitution führen.
In der Haushaltstheorie wird die GRS auch verwendet, um das Konsumverhalten von Individuen zu erklären, insbesondere im Hinblick auf die Nachfrageelastizität bzw. Preiselastizität der Nachfrage. Wenn die GRS hoch ist, sind Individuen bereit, schnell von einem Gut auf ein anderes umzusteigen, wenn sich die Preise ändern. Wenn die GRS niedrig ist, werden Individuen weniger bereit sein, von einem Gut auf ein anderes umzusteigen, wenn sich die Preise ändern.
Insgesamt spielt die GRS also eine wichtige Rolle in der Haushaltstheorie, da sie hilft, die Entscheidungsfindung von Individuen und ihre Reaktion auf Veränderungen in den Preisen und Einkommen zu verstehen. Sie ist eng verbunden mit Indifferenzkurve und der Preiselastizität der Nachfrage.
Was ist der Zusammenhang zwischen der Grenzrate der Substitution und der Indifferenzkurve?
Die Grenzrate der Substitution (GRS) und die Indifferenzkurve stehen in engem Zusammenhang und sind wichtige Konzepte in der mikroökonomischen Theorie der Entscheidungsfindung von Individuen.
Die Indifferenzkurve beschreibt grafisch alle möglichen Kombinationen von zwei Gütern, die für das Individuum gleich attraktiv sind. Sie gibt somit die Präferenzen des Individuums wieder. Eine höhere Indifferenzkurve zeigt dabei eine höhere Gesamtpräferenz an, da sie mehr von beiden Gütern beinhaltet.
Die GRS hingegen gibt an, wie viel von einem Gut durch ein anderes ersetzt werden kann, während der Nutzen konstant bleibt. Es beschreibt also, wie viel eines Gutes das Individuum bereit ist aufzugeben, um eine zusätzliche Einheit des anderen Gutes zu erhalten.
Die GRS kann grafisch durch die Steigung der Indifferenzkurve an einem bestimmten Punkt gemessen werden. An einem Punkt auf der Indifferenzkurve haben beide Güter den gleichen Nutzen, und somit ist die Steigung der Indifferenzkurve an diesem Punkt gleich der GRS. Die GRS gibt also an, wie viel das Individuum von einem Gut aufgeben muss, um eine zusätzliche Einheit des anderen Gutes zu erhalten, während es immer noch den gleichen Nutzen hat.
Zusammenfassend ist die Indifferenzkurve ein Konzept, das die Präferenzen des Individuums widerspiegelt, während die GRS die Bereitschaft des Individuums beschreibt, von einem Gut auf ein anderes umzusteigen, um den Nutzen konstant zu halten. Die GRS kann anhand der Steigung der Indifferenzkurve gemessen werden, was eine wichtige Anwendung der beiden Konzepte in der Mikroökonomie darstellt.
Eigenschaften der Grenzrate der Substitution
Die Grenzrate der Substitution (GRS) hat verschiedene Eigenschaften, darunter:
GRS und Güterart: Kann die Grenzrate der Substitution positiv sein?

Im Normalfall ist die Grenzrate der Substitution negativ.
Dies ergibt sich dadurch, dass man normalerweise davon ausgeht, dass der Konsum eines Gutes mit steigendem Preis bzw. sinkenden Einkommen abnimmt. Allerdings gibt es von dieser Regel Ausnahmen, wenn die (relativen) Präferenzen des Konsumenten für ein Gut von dieser Regel abweichen. Dies ist vor allem bei einem inferiorem Gut und dem Giffen-Gut der Fall. Hier ist die Grenzrate der Substitution positiv. Wir fassen die verschiedenen Güterarten und die zugehörigen GRS aus der Übersicht noch einmal zusammen:
Normales Gut und superiores Gut: Ein normales Gut ist ein Gut, bei dem die Nachfrage steigt, wenn das Einkommen des Konsumenten steigt, aber nicht so stark wie bei einem Superior-Gut. Ein normales Gut ist also weder inferioren noch superior.
Für ein normales Gut gilt, dass die GRS negativ ist, aber nicht so stark negativ wie bei einem Superior-Gut. Das bedeutet, dass das Individuum bereit ist, weniger von einem Gut aufzugeben, um eine zusätzliche Einheit des anderen Gutes zu erhalten, wenn sein Einkommen steigt. Allerdings ist die Bereitschaft, dies zu tun, nicht so groß wie bei einem Superior-Gut.
Insgesamt lässt sich sagen, dass die Art des Gutes einen Einfluss auf die GRS hat, aber dieser Einfluss hängt von der Veränderung der Präferenzen des Individuums bei einer Änderung des Einkommens ab.
Ein inferiores Gut ist ein Gut, bei dem die Nachfrage abnimmt, wenn das Einkommen des Konsumenten steigt. Ein klassisches Beispiel für ein inferiores Gut ist Reis: Wenn das Einkommen eines Konsumenten steigt, ersetzt er Reis durch teurere Güter wie Fleisch oder Fisch.
Im Falle eines inferioren Gutes ist die GRS positiv. Das bedeutet, dass das Individuum bereit ist, mehr von einem Gut aufzugeben, um eine zusätzliche Einheit des anderen Gutes zu erhalten. Mit anderen Worten, das Individuum ist bereit, mehr Reis aufzugeben, um eine zusätzliche Einheit Fleisch oder Fisch zu erhalten, wenn sein Einkommen steigt.
Giffen-Gut: Ein Giffen-Gut ist ein sehr ungewöhnlicher Fall, der in der Praxis selten vorkommt. Es handelt sich um ein inferiores Gut, bei dem die Nachfrage steigt, wenn der Preis des Gutes steigt. Das bedeutet, dass die Konsumenten mehr von diesem Gut kaufen, wenn der Preis steigt und weniger, wenn der Preis sinkt.
Für ein Giffen-Gut gilt, dass die GRS positiv ist. Das bedeutet, dass das Individuum bereit ist, mehr von einem Gut aufzugeben, um eine zusätzliche Einheit des anderen Gutes zu erhalten, wenn der Preis des Giffen-Gutes steigt. Dies ist ein ungewöhnlicher Fall, da die meisten Güter eine negative GRS haben.
Vollkommene Substitutionsgüter: Zwei Güter, bei denen die Grenzrate der Substitution des einen durch das andere konstant ist.
Vollkommene Komplementärgüter: Zwei Güter, bei denen die GRS unendlich oder gleich null ist, die Indifferenzkurven bilden einen rechten Winkel.
Ungut: Güter, bei denen eine geringere Menge einer größeren Menge vorgezogen wird. Durch „Uminterpretation“ des Ungutes, besitzt auch das Ungut eine negative GRS.
Wie berechnet und zeichnet man die Grenzrate der Substitution?
1. Vorgehen zur Berechnung der Grenzrate der Substitution
Um die Grenzrate der Substitution (GRS) zu berechnen, müsst ihr zuerst die Grenznutzen beider Güter berechnen. Angenommen, ihr habt den Nutzen einer bestimmten Menge von Gut 1 und Gut 2 gemessen und möchtet nun die GRS berechnen. Die Schritte wären wie folgt:
Schritt 1: Berechnung des Grenznutzens von Gut 1 und Gut 2, indem ihr die partielle Ableitung des Nutzens nach jedem Gut berechnet:
MU_{1}=\frac{\text{d}U}{\text{d}Gut_{1}}
MU_{2}=\frac{\text{d}U}{\text{d}Gut_{2}}
Schritt 2: Teilt den Grenznutzen von Gut 1 durch den Grenznutzen von Gut 2:
GRS = \frac{MU_{1}}{MU_{2}}
Schritt 3: Multipliziert das Ergebnis mit einem negativen Vorzeichen, um anzuzeigen, dass die GRS abnimmt, wenn der Konsum von Gut 2 zunimmt:
GRS = - \frac{MU_{1}}{MU_{2}}
Dabei ist zu beachten, dass die GRS von der gegebenen Menge an Gütern und der Nutzenfunktion abhängig ist und somit für verschiedene Individuen und Situationen unterschiedlich sein kann.
2. Beispiele zur Berechnung der Grenzrate der Substitution
Nachdem wir nun das generelle Vorgehen zur Berechnung der GRS kennen, zeigen wir euch an zwei gängigen Nutzenfunktionen beispielhaft, wie man diese Schritte umsetzt. Der Vielfalt der Ausgestaltung der Nutzenfunktionen, die euch tatsächlich in Schule, Studium etc. in Aufgaben begegnen können, sind hierbei keine Grenzen gesetzt. Wenn ihr das System verstanden habt, werdet ihr aber, mit etwas Übung und ein paar Kenntnissen über Ableitungsregeln, keine Schwierigkeiten haben.
Beispiel 1: Cobb-Douglas-Nutzenfunktion und Grenzrate der Substitution
U(x,y) = x^{0,5}*y^{0,5}
Die GRS an der Stelle (x,y) kann für diese Funktion berechnet werden, indem ihr das Verhältnis der partiellen Ableitungen der Nutzenfunktion nach x und y bildet:
1. Partielle Ableitung nach x:
\frac{\partial U}{\partial x}= 0,5*x^{-0,5}*y^{0,5}
2. Partielle Ableitung nach y:
\frac{\partial U}{\partial y}= 0,5*x^{0,5}*y^{-0,5}
3. Bildung des Verhältnisses der Ableitungen:
GRS =-\frac{MU_{1}}{MU_{2}} = -\frac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}} =-\frac{0,5*x^{-0,5}*y^{0,5}}{0,5*x^{0,5}*y^{-0,5}}
Beispiel 2: Lineare Nutzenfunktion und Grenzrate der Substitution
U (x,y) = ln(x) + ln(y)
Die GRS an der Stelle (x,y) könnt ihr berechnen, indem ihr wieder das Verhältnis der partiellen Ableitungen der Nutzenfunktion nach x und y bildet:
1. Partielle Ableitung nach x:
\frac{\partial U}{\partial x} = 1/x
2. Partielle Ableitung nach y:
\frac{\partial U}{\partial y} = 1/y
3. Bildung des Verhältnisses der Ableitungen:
GRS =-\frac{MU_{1}}{MU_{2}} = -\frac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}} =-\frac{1/x}{1/y} = -(y/x)
Zur Erinnerung: Aufgrund der negativen Steigung („Austauschverhältnis“!), besitzt die GRS ein negatives Vorzeichen. Auch, wenn die einzelnen Ableitungen positiv sind.
In beiden Beispielen ist die GRS am Punkt (x,y) gleich der Steigung der Indifferenzkurve an diesem Punkt. Wenn wir also die GRS an verschiedenen Punkten der Indifferenzkurve berechnen, könnt ihr so die gesamte Indifferenzkurve darstellen und damit die Präferenzen des Konsumenten beschreiben.
3. Grafische Darstellung der Grenzrate der Substitution
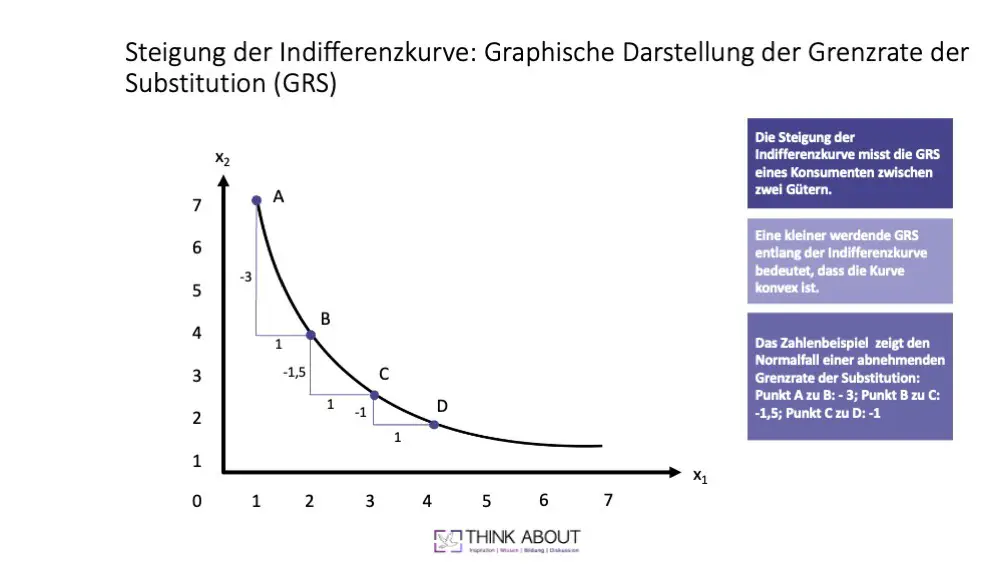
In der Grafik seht ihr für eine nicht näher spezifizierte Nutzenfunktion die Indifferenzkurve eines Konsumenten für zwei Güter x1 und x2 und die sich ergebende Grenzrate der Substitution.
Die Kurve weist einen fallenden Verlauf auf und über die Steigung könnt ihr die Grenzrate der Substitution messen. In der Grafik ist dies beispielhaft mit vier Punkten dargestellt. Betrachtet ihr die Punkte A bis D seht ihr, dass die GRS immer kleiner wird. Dies zeigt, dass die Indifferenzkurve konvex ist.
Ihr seht, dass es verschiedene Möglichkeiten gibt, die Grenzrate der Substitution zu bestimmen. Ihr könnt sie einmal über die Nutzenfunktion berechnen. Oder, wie hier, wenn euch eine Kurve (mit Zahlen) gezeigt wird, über die Bewegung von einem Punkt auf der Kurve zu einem anderen Punkt ablesen. Das Vorgehen ist ähnlich, wie wir es in unserer Erklärung zur Preiselastizität der Nachfrage beschrieben haben.
Theorie und Praxis: Herausforderung bei der Berechnung und Interpretation der Grenzrate der Substitution
Bislang haben wir euch beschrieben, wie ihr die Grenzrate der Substitution berechnen und zeichnen könnt. Insbesondere am Anfang kann es leicht passieren, dass man bei den vielen Übungsaufgaben übersieht, welchen Sinn das Ergebnis eigentlich hat.
Wir möchten euch deshalb zum Abschluss des Artikels noch einmal kurz zusammenfassen, auf welche Punkte und ökonomischen Zusammenhänge ihr achten solltet, wenn ihr die GRS berechnet. Und um euch zu zeigen, dass die GRS nicht nur in der Mikro 1-Vorlesung auftaucht, enden wir mit den Herausforderungen, die euch begegnen, wenn ihr die GRS mit „realen“ Daten im Rahmen empirischer Arbeiten berechnen und schätzen wollt.
Checkliste: Auf diese Faktoren solltet ihr bei der Interpretation der Grenzrate der Substitution achten:
Grenzrate der Substitution und Empirie: Herausforderungen bei der praktischen Berechnung
Insgesamt erfordert die Berechnung der GRS sorgfältige Analyse und kann mit einigen Herausforderungen verbunden sein, aber sie ist dennoch ein nützliches Instrument zur Analyse von Konsumenten- und Produktionsentscheidungen. Die wichtigsten Herausforderungen sind:
