Die Quantitätsgleichung des Geldes stellt den Zusammenhang zwischen Geld- und Gütermarkt dar. In diesem Artikel stellen wir euch die Gleichung, ihre Bestandteile und ihre Entwicklung vor. Außerdem erklären wir euch den kleinen, aber feinen Unterschied zwischen der Quantitätsgleichung und der Quantitätstheorie des Geldes.
Definition
Quantitätsgleichung des Geldes: auch als Fisher‘sche Verkehrsgleichung bekannt. Sie beschreibt die Identität zwischen der Güter- und Geldseite eines Kaufes bzw. Verkaufes. Sie verbindet damit den Güter- und Geldmarkt infolge einer Markttransaktion, bei der Waren gegen einen Geldbetrag getauscht werden.
M\ \times \ v\ =\ P\ \times \ Y
Geldmarkttransaktion = Gütermarkttransaktion
Hinweis: Die Quantitätsgleichung bzw. Fisher’sche Verkehrsgleichung ist nicht mit der sogenannten Fisher Gleichung zu verwechseln. Erstere bezieht sich auf die Identität zwischen Geld- und Gütermarkt. Letztere beschreibt den Zusammenhang zwischen Zinsen und Inflation.
Historie: Entwicklung der Quantitätsgleichung
Die Quantitätsgleichung des Geldes ist die Grundlage, auf der die sogenannte Quantitätstheorie des Geldes entwickelt wurde. Beginnend mit der „Klassik“ im 18. Jahrhundert fingen vermehrt Philosophen und Gelehrte an, sich systematisch mit ökonomischen Fragen zu beschäftigen und darüber zu forschen. Diese ersten Forschungsansätze basierten auf immer wiederkehrenden Beobachtungen. Eine dieser ökonomischen Beobachtungen war, dass das Preisniveau schwankte. Mit anderen Worten: Die klassischen Gelehrten beobachteten das Auftreten von Inflation und ihre negativen Folgen und suchten hierfür nach Erklärungsansätzen.
Der verbal beschriebene Ansatz von David Hume besagt, dass jede Preisveränderung aus einer Änderung der Geldmenge resultiert. Diese Erklärung bezeichnet man als Quantitätstheorie des Geldes.
Irving Fisher übersetzte den Erklärungsansatz von Hume schließlich in eine Gleichung. Diese erste Version der Quantitätsgleichung bzw. Fisher’sche Verkehrsgleichung bildet die Grundlage aller folgenden Weiterentwicklungen der Quantitätsgleichung und damit auch der Quantitätstheorie.
Wichtige Weiterentwicklungen und damit auch Versionen der Quantitätsgleichung sind die sogenannte Einkommensversion und später die cambridge-Gleichung von Alfred Marshall.
Die Entwicklung der Quantitätsgleichung und der Quantitätstheorie mündet schließlich in den Arbeiten von Milton Friedman. Mit seiner „Neoquantitätstheorie“ des Geldes und der damit einhergehenden Gleichung schloss er die Erklärungslücken, welche die bisherigen Erklärungsansätze bei der Identität von Geld- und Gütermarkt basierend auf den Bestandteilen der Gleichung nicht erklären konnten.
Die Quantitätsgleichung und die Quantitätstheorie des Geldes
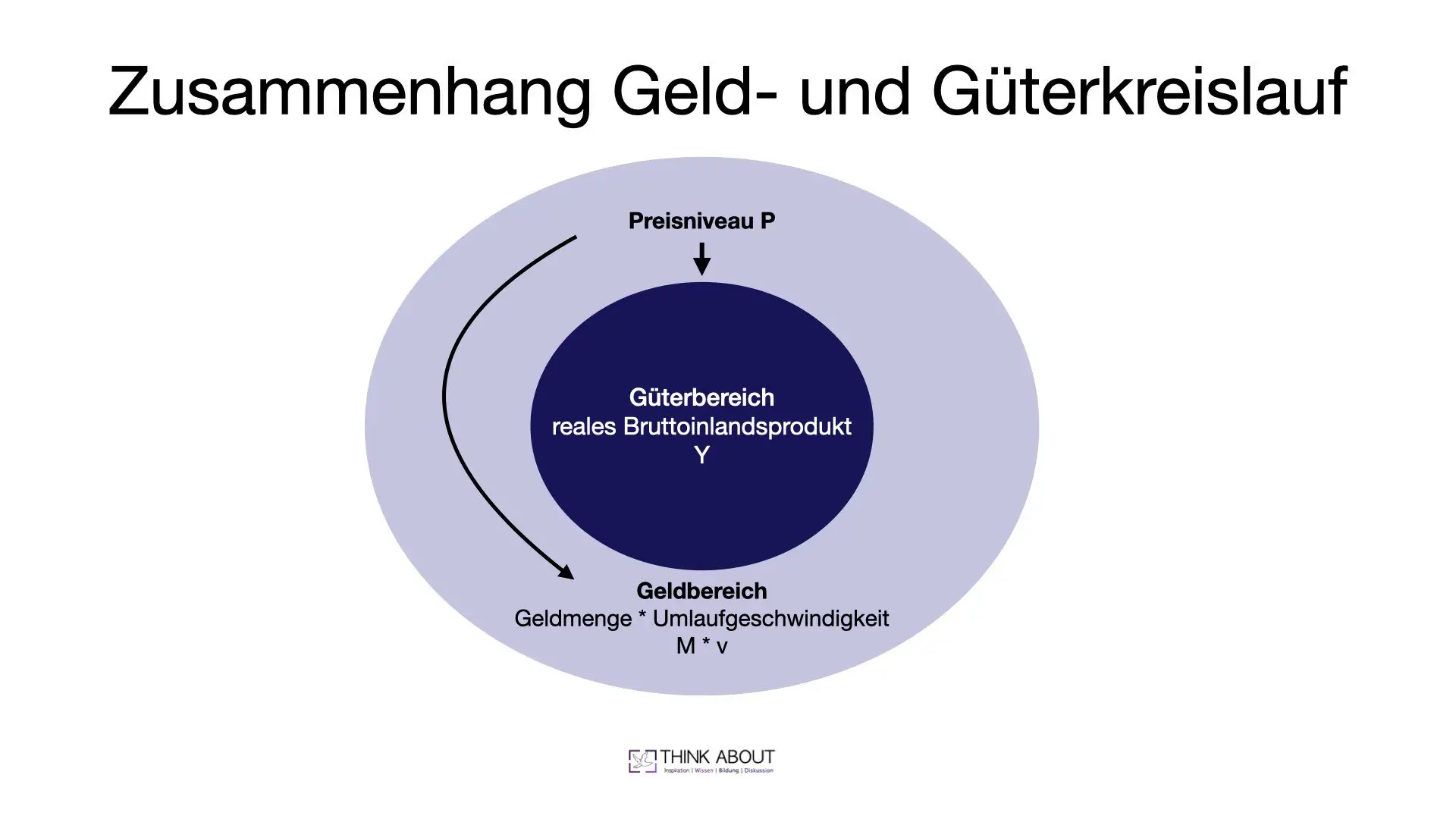
Die Grafik illustriert den Zusammenhang zwischen Geld- und Gütermarkt, der sich aus den vier Bestandteilen der Quantitätsgleichung ergibt.
Quantitätsgleichung: M\ \times \ v\ =\ P\ \times \ Y
M = Geldmenge
v = Umlaufgeschwindigkeit des Geldes
P = Preisniveau
Y bzw. Y{}^{r} = reales Bruttoinlandsprodukt
Der Geldbereich bzw. der Geldmarkt ist charakterisiert durch die Geldmenge multipliziert mit der Umlaufgeschwindigkeit des Geldes (M * v).
Das (reale) BIP stellt den Güterbereich bzw. Gütermarkt dar. P ist das durchschnittliche Preisniveau P.
Die Quantitätsgleichung beruht auf der Annahme, dass alle ökonomischen Transaktionen Y über eine bestimmte festlegbare Geldmenge M abgewickelt werden. Diese Geldmenge wechselt infolge der Transaktionen mehrfach den Besitzer. Die Anzahl dieser Wechsel in einem definierten Zeitraum misst die Umlaufgeschwindigkeit v.
Die Quantitätsgleichung ist definitionsgemäß immer wahr und kann empirisch nicht falsifiziert werden.
Trifft man einige Annahmen und formt die Gleichung um, gelangt man zur Quantitätstheorie.
Drückt man die Qualitätsgleichung in Veränderungsraten dar, erhält man folgenden Ausdruck:
\widehat{M} \ \times \ \ \widehat{v} =\ \ \widehat{P} \times \ \widehat{Y}
Löst man die Gleichung nun nach P auf, erhält man:
P\ =\ \frac{M\times v}{Y}
Aus der Quantitätsgleichung kann somit abgeleitet werden, wie Inflation entsteht. Wächst die Geldmenge schneller als das Einkommen, führt dies ceteris paribus zu Inflation.
In diesem Sinne kann die Quantitätsgleichung über das unterschiedliche Wachstum zweier Kerndeterminanten von Geld- und Gütermarkt erklären, wie es zu Inflation kommt.
Somit ist man bei der Quantitätstheorie angelangt. Hiernach bestimmt die Geldmenge direkt das Preisniveau, ohne Auswirkungen auf die Realwirtschaft.
Die Quantitätsgleichung ist damit die Grundlage der Quantitätstheorie. Sie dient als Ausgangspunkt für geldpolitische Maßnahmen im Rahmen von Konjunktur- und Stabilisierungspolitik. Zudem ist sie der älteste Ansatz zur Erklärung von Inflation, nämlich der Geldmengeninflation.
Entwicklung: Versionen der Quantitätsgleichung des Geldes
1. Ursprung: Transaktionsversion
Fisher'sche Verkehrsgleichung: M\ \times \ v\ =\ Q\ \times \ P
Die Grundlage der heute bekannten Quantitätsgleichung des Geldes stellt die Fisher’sche Verkehrsgleichung dar. Diese Ursprungsversion bezeichnet man auch als Transaktionsversion.
Die Bestandteile der Gleichung sind sehr ähnlich, wie die oben beschriebenen Faktoren. Gemeinsam beschreiben die Bestandteile die Geld- und Güterseite einer Transaktion. Der entscheide Unterschied zwischen der Fisher’schen Verkehrsgleichung und den späteren Versionen besteht in der Interpretation des Transaktionsvolumens auf dem Gütermarkt.
In der Gleichung wird dies durch den Buchstaben Q repräsentiert.
Q = Gesamtwirtschaftliche Gütermenge
Hierbei ist zu beachten, dass es sich bei dieser Definition wirklich um die gesamte Gütermenge handelt und somit sämtliche Transaktionen in der Gleichung abgebildet werden.
Das bedeutet z.B., wenn ein Haus dreimal verkauft wird, entspricht dies drei Transaktionen. Q beinhaltet damit dreimal den Wert des Hauses.
Multipliziert mit P, dem Durchschnittspreis aller Güter, ergibt sich das nominale Transaktionsvolumen einer Volkswirtschaft.
Die linke Seite der Gleichung beschreibt wie gehabt die Finanzierung der Transaktion über den Geldmarkt. M ist die Geldmenge und v die Umlaufgeschwindigkeit.
Zu beachten ist bei der Fisher’schen Verkehrsgleichung, dass sie per Definition immer wahr ist. Sie kann nicht widerlegt werden, da sich Geld- und Güterseite wertmäßig immer entsprechen müssen.
Die Gleichung stellt damit nur einen Zusammenhang dar und beinhaltet damit noch keine Erklärung, warum die Gleichung so ist wie sie ist.
Formuliert man die Gleichung z.B. nach v um, erhält man:
v\ =\ \frac{Q\times P}{M}
In dieser Form würde die Gleichung dann die Umlaufgeschwindigkeit des Geldes definieren. Die Geldumlaufgeschwindigkeit ist demnach eine Funktion zwischen nominalen Gütervolumen einer Volkswirtschaft und der vorhandenen Geldmenge.
Ähnliche Umformungsmöglichkeiten bestehen für jede der vier Bestandteile.
In den Weiterentwicklungen der Fisher’schen Verkehrsgleichung werden nun sukzessive die „Probleme“ dieser Gleichung analysiert und versucht zu lösen. Die frühesten Kritikpunkte an der Ursprungsgleichung betrafen hierbei die Messung des Transaktionsvolumens Q*P.
Kritikpunkte an der Transaktionsversion:
- Keine klare Definition und Abgrenzung der Größen „Transaktionsvolumen“ und „allgemeines Preisniveau“
- Mit dem vorhandenen Datenmaterial der volkswirtschaftlichen Gesamtrechnung können die beiden Größen nur unzureichend erfasst werden
- Somit ist eine empirische Überprüfung der Gleichung kaum möglich.
2. Weiterentwicklung: Einkommensversion und velocity Ansatz
Irving Fisher nahm die grundlegenden Kritikpunkte an seiner Verkehrsgleichung auf und definierte die beiden Parameter für den Gütermarkt um.
Hierdurch gelangt man zur sogenannten Einkommensversion der Quantitätsgleichung des Geldes.
Die weiterentwickelte Gleichung lautet:
M\ \times \ v\ =Y^{r}\times \ P
Statt des gesamten Transaktionsvolumens Q und des Durchschnittspreises der Güter bildet man den Gütermarkt nun durch die wertschöpfenden Transaktionen, gemessen durch das Einkommen, und den dazugehörigen Einkommenspreisindex P ab.
Yr fällt damit in der Regel kleiner aus als Q.
Obwohl die Gleichung fast genauso lautet wie die Ursprungsversion, sind die Bedeutung und damit Interpretation der Bestandteile nun nicht mehr vergleichbar, mit Ausnahme der Geldmenge M.
Yr = errechnet sich aus der volkswirtschaftlichen Gesamtrechnung. Es enthält nur noch wertschöpfende Gütertransaktionen und entspricht damit dem realen Volkseinkommen. Verwendet wird in der Regel das reale BIP.
P = Preisindex zur Ermittlung des Volkseinkommens zu konstanten Preisen. Quelle ist hierfür ebenfalls die Volkswirtschaftliche Gesamtrechnung, wodurch eine methodisch und statistisch gute Qualität gesichert ist. Verwendet wird der BIP-Deflator.
v = Einkommenskreislaufgeschwindigkeit des Geldes. Sie misst, wie oft eine Geldeinheit in einem bestimmten Zeitraum durchschnittlich genutzt wird, einen Betrag zum Volkseinkommen zu finanzieren. Die Änderung der Definition von v ist eine Folge der geänderten Messung der Güterseite.
M bleibt in seiner Messung und damit Interpretation unverändert.
Kritikpunkte an der Einkommensversion:
- Weiterhin ist nicht möglich, eine kausale Beziehung zwischen den einzelnen Bestandteilen herzuleiten.
- Hierzu müssen Annahmen über die einzelnen Bestandteile getroffen werden.
- Fisher unternahm hierzu einen ersten Ansatz mit seinem sogenannten „velocity approach.“
Fishers Velocity Ansatz:
Er nahm an, dass die Geldumlaufgeschwindigkeit v im Zeitablauf konstant ist, da sie auf den Zahlungsgewohnheiten der Wirtschaftssubjekte beruht.
Die Quantitätsgleichung des Geldes lautet mit dieser Annahme:
M\ \times \ \overline{v} \ =Y{}^{r}\ \times \ P
Wenn man nun annimmt, dass die Geldmenge M von der Zentralbank gesteuert wird, kann nun die These formuliert werden, dass hieraus eine Erhöhung des nominalen Volkseinkommens resultiert (Yr * P, NICHT Yr!). Die These beruht auf der damals vorherrschenden Meinung der klassischen Dichotomie zwischen Geld- und Gütermarkt. Im Kern sagt die klassische Dichotomie aus, dass Produktion und Beschäftigung nur auf dem Gütermarkt beeinflusst werden, und nicht durch Vorkommnisse auf dem Geldmarkt.
Die Erhöhung der Geldmenge führt damit nicht zu einer Änderung bei Yr, sondern bei P. Und hierüber zu einer Erhöhung des nominalen Volkseinkommens Yr * P.
Zusammengefasst formuliert der velocity Ansatz von Fisher über die Annahme zu v, dass eine proportionale Beziehung zwischen der gesamtgesellschaftlichen Geldmenge und dem Preisniveau besteht.
Insofern bildet diese Version der Quantitätsgleichung des Geldes den monetären Erklärungsansatz für Inflation.
Was diese Version der Quantitätsgleichung damit aber nicht ermöglicht, ist eine Erklärung der Geldnachfrage.
3. Marshall: Cambridge-Version
Die Erklärung der Geldnachfrage über die Quantitätsgleichung gelang Alfred Marshall. Seine Version der Quantitätsgleichung des Geldes ist unter dem Namen „Cambridge cash-balance approach“ oder als Kassenhaltungsansatz bekannt.
Im Prinzip unterscheidet sich sein Ansatz kaum von der Einkommensversion der Quantitätstheorie. Allerdings interpretiert die Determinante v um. Seine Version leitet sich wie folgt her. In einem ersten Schritt löst er die Quantitätsgleichung des Geldes nach der Geldmenge M auf:
M\ \times \ v\ =Y{}^{r}\ \times \ P
M\ =\ \frac{1}{v} \ \times \ P\ \times \ Y\ ^{r}
Seine Neuerung besteht nun im Umgang mit dem Kehrwert von v bzw. mit dem Wert 1/v.
Es gilt nun:
k\ =\ \frac{1}{v}
M\ =\ k\ \times \ P\ \times \ Y^{r}
k ist der sogenannte Kassenhaltungskoeffizient bzw. das „cambridge k“.
Durch diese vermeintlich kleine Änderung ergibt sich eine völlige neue Interpretation dieser Version der Quantitätsgleichung des Geldes.
Die rechte Seite beschreibt jetzt die gewünschte Kassenhaltung k, welche die Wirtschaftssubjekte für ihre Transaktionen p*Yr benötigen. Mit anderen Worten: Wie viel Bedarf an Geld besteht, um die Transaktionen auf dem Gütermarkt durchführen zu können.
Auf der linken Seite steht mit der Geldmenge M, das für die Transaktionen zur Verfügung stehende Geld.
So kann man die cambridge Version der Quantitätsgleichung des Geldes als Gleichgewichtsbedingung für den Geldmarkt interpretieren:
Die linke Seite stellt das Geldangebot dar. Die rechte Seite beschreibt die Geldnachfrage. Da der Kassenhaltungskoeffizient k nicht direkt beobachtet wird, sondern sich aus dem Wert 1/v ergibt, beschreibt der Wert die gewünschte Kassenhaltung. Es handelt sich damit um einen änderbaren Parameter. Somit stellt die rechte Seite der Gleichung auch nicht einfach nur die (konstante) Geldnachfrage dar, sondern eine Geldnachfragefunktion.
Mit dieser Gleichung kann dann auch die LM-Kurve problemlos hergeleitet werden.
Dass nicht nur die Geldnachfrage, sondern auch das Geldangebot eine Funktion von Parametern ist. Diese Forschungslücke wurde dann später von Milton Friedman in der sogenannten Neo-Quantitätstheorie des Geldes gefüllt.
Volkswirtschaftliche Bedeutung der Quantitätsgleichung
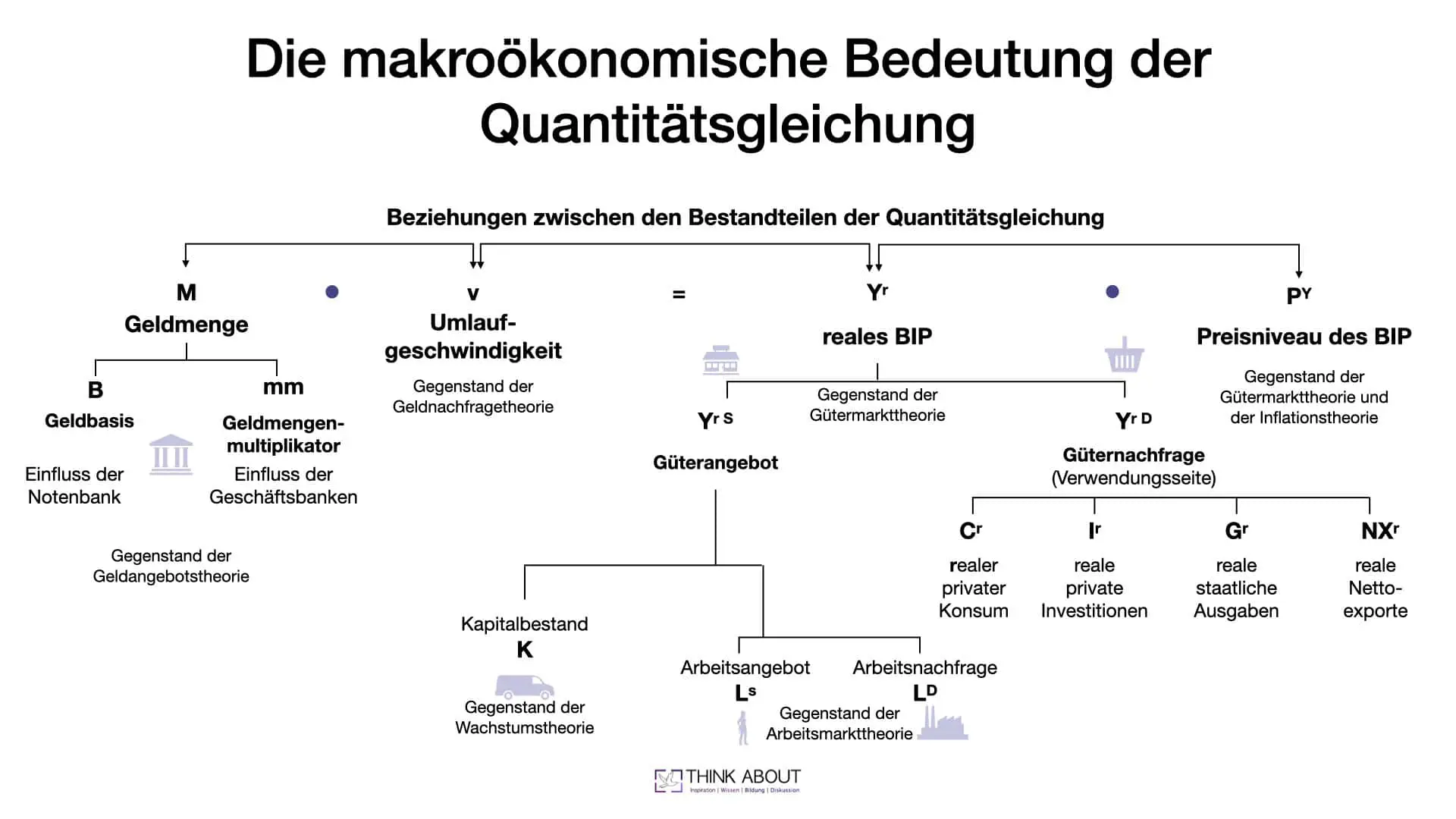
Die Weiterentwicklungen der Quantitätsgleichung zeigen, wie man mittels Annahmen von einer Gleichung zu einer Theorie gelangte.
Die getroffenen Annahmen in der Einkommensversion ermöglichten mit Hilfe der Quantitätsgleichung eine Erklärung für das Auftreten von Inflation.
Die cambridge-Version erlaubt aus der Quantitätsgleichung das Gleichgewicht auf dem Geldmarkt darzustellen, sowie eine Geldnachfragefunktion herzuleiten.
Die Grafik stellt nun zusammenfassend die makroökonomische Bedeutung der Quantitätsgleichung in ihrer aktuellen Form dar.
Sie geht damit über die Inhalte in diesem Artikel hinaus. Da wir hier nicht die Neoquantitätstheorie von Milton Friedman vorgestellt haben, in der die Geldangebotsseite behandelt wird.
Dennoch veranschaulicht die Grafik sehr gut, wie über die Quantitätsgleichung und der hier dargestellte Zusammenhang zwischen Güter- und Geldmarkt auf die verschiedensten makroökonomischen Zusammenhänge geschlossen werden kann.
Geht man von den vier Determinanten aus, ist das Preisniveau Gegenstand der Gütermarkttheorie und der Inflationstheorie.
Das BIP (Y) kann angebotsseitig oder nachfrageseitig interpretiert werden. Dementsprechend wird es dann auch von verschiedenen Determinanten beeinflusst.
Nachfrage (Verwendungsseite des BIP) Y = C + I + G + NX
Die (realen) Nettoexporte sind der Außenbeitrag.
Die Angebotsseite des BIP entspricht dem Güterangebot und wird durch die Auslastung der Produktionsfaktoren Kapital und Arbeit beeinflusst. Beide Produktionsfaktoren unterliegen wieder weiteren Einflüssen.
Auf der Geldseite sehen wir, dass das Geldangebot M und die Umlaufgeschwindigkeit v ebenfalls Gegenstand eigener Theorien sind und beeinflusst werden.
Diese tiefen Verästelungen der Quantitätsgleichung in die verschiedenen makroökonomischen Teilgebiete belegen ihre Bedeutung für die angewandte Forschung und auch politische Praxis. Etwa das Ableiten von konjunkturpolitischen Instrumenten. Hohe Beschäftigung, ein stabiles Preisniveau und ein angemessenes Wachstum sind die stabilitäts- bzw. konjunktur- und wachstumspolitischen Aufgaben des Staates (Stichwort: magisches Viereck). Mit Hilfe der Quantitätsgleichung und der in der Grafik dargestellten Verbindungen gelangt man zu allen „Märkten“ und Teilgebieten, die in der Stabilitätspolitik bei der Entscheidungsfindung beachtet werden müssen.
Zusammenfassung
- Quantitätsgleichung des Geldes: M*v = P*Y
- Die erste Version ist die Fisher’sche Verkehrsgleichung. Die Einkommensversion ist die heute gebräuchlichste Version der Gleichung.
- Die Quantitätsgleichung ist eine Identität und keine Theorie, da keine Annahmen über das Verhalten der vier Determinanten bestehen.
- Die Weiterentwicklungen treffen diese Annahmen. Hierüber bietet die Quantitätsgleichung Erklärungen für Inflation und die Geldnachfragefunktion.
- Aufgrund ihrer Vielseitigkeit bietet die Gleichung einen Ausgangspunkt für stabilitäts- und konjunkturpolitische Analysen.
