Die Fisher-Gleichung besagt, dass der Nominalzinssatz der Summe aus Realzinssatz und Inflationsrate entspricht. In diesem Artikel erklären wir euch Definition, Bedeutung und Annahmen der Gleichung. Wir zeigen euch, wie man die Gleichung herleitet und wie sich die Fisher-Gleichung vom Fisher-Effekt abgrenzt.
Definition
Fisher-Gleichung: i=r+\pi.
Der Nominalzinssatz i ergibt sich aus der Summe des realen Zinssatzes r und der Inflationsrate \pi.
Die Gleichung stellt damit über die Zinsen einen Zusammenhang zwischen dem Geldmarkt und dem Gütermarkt dar. Nach dieser Gleichung bestimmen zwei Determinanten den Nominalzinssatz: der Realzinssatz und die Inflationsrate. D.h. eine Änderung des Nominalzinssatzes kann auf Änderungen des Realzinssatzes und/oder der Inflationsrate zurückzuführen sein.
Von der Fisher-Gleichung ist der Fisher-Effekt abzugrenzen. Dies ist an dieser Stelle relevant, da sich Gleichung und Effekt auf dieselbe mathematische Formulierung der Fisher-Gleichung beziehen.
Fisher-Effekt: Es besteht eine Eins-zu-Eins-Beziehung zwischen dem Nominalzinssatz i und der Inflationsrate \pi.
Das bedeutet: Steigt der Nominalzinssatz um z.B. 1 Prozentpunkt, steigt die Inflationsrate ebenfalls um 1 Prozentpunkt.
Die Fisher-Gleichung und die Quantitätsgleichung bzw. Theorie des Geldes erklären zusammen, wie es zu dem Fisher-Effekt kommt.
Man kann auch sagen: Die Fisher-Gleichung ist die theoretische Herleitung des Fisher-Effektes. In der Forschungspraxis trennt man deshalb nicht konkret zwischen den beiden Begriffen. Wenn man versucht, den Zusammenhang zwischen Inflation und Zinsen empirisch zu belegen, bedeutet dies, dass man versucht, in Daten einen Fisher-Effekt zu beobachten oder zu schätzen.
Statistik: Inflation und Zinsen
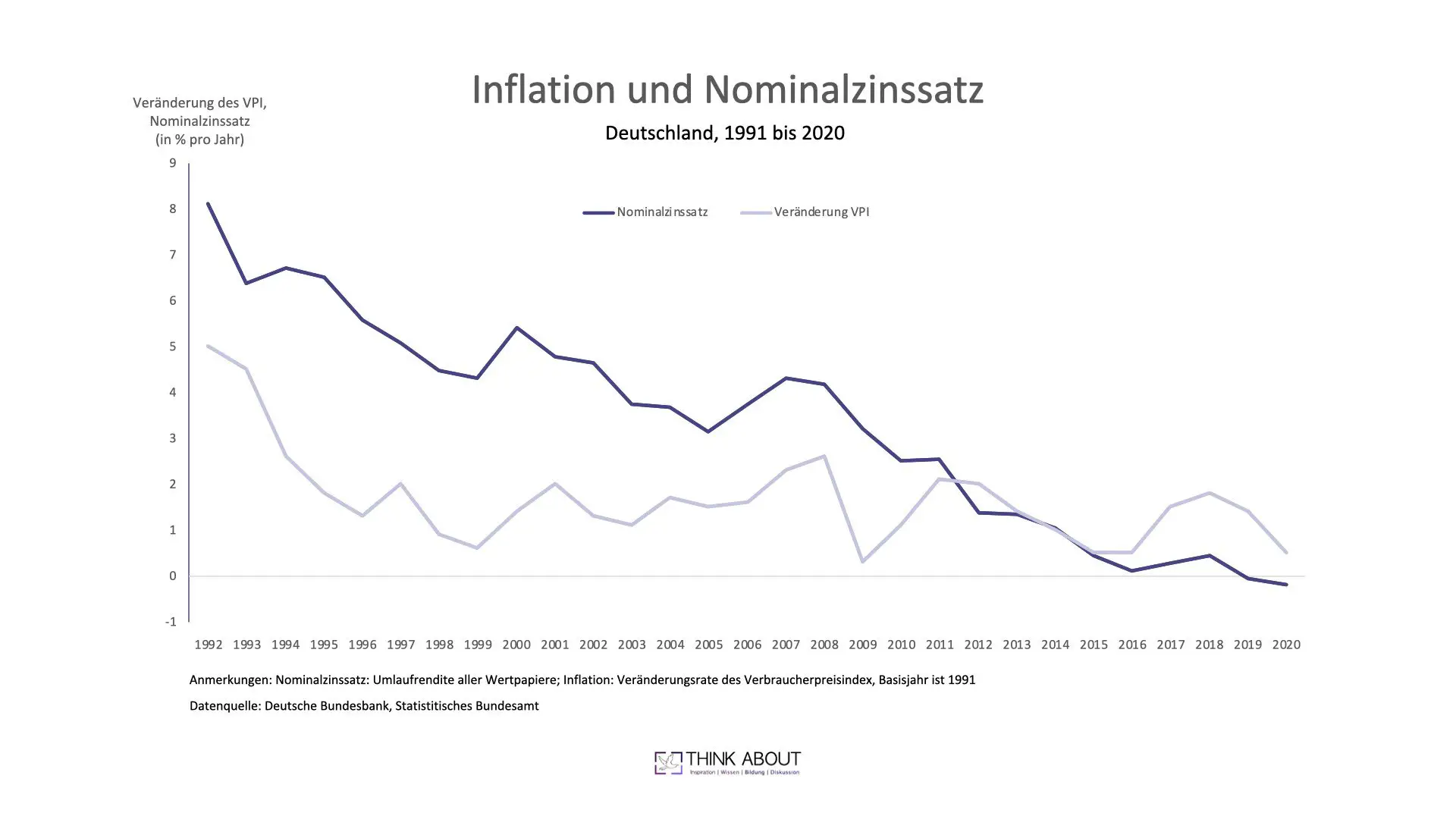
Die Grafik stellt den Zusammenhang von Inflation und Nominalzinssatz für Deutschland dar. Es ist der Zeitraum 1992-2020 abgebildet, um einen etwaigen „Wiedervereinigungseffekt“ auszuschließen. Die Inflationsrate wird über den Verbraucherpreis des statistischen Bundesamtes (VPI) gemessen. Als Variable für den Nominalzinssatz haben wir die Umlaufrendite aller Wertpapiere verwendet.
Zwischen 1992 und 2010 ist eindeutig ein Fisher-Effekt erkennbar: Eine niedrigere Inflationsrate führt zu einem niedrigeren Nominalzinssatz.
Im Rahmen der Entwicklungen in Folge der Wirtschaftskrise 2008/2009 hat sich dieser Zusammenhang etwas konfus entwickelt. Insbesondere seit 2015 haben wir nun ein umgekehrtes Verhältnis: Die Inflationsrate liegt höher als der Nominalzinssatz.
Es bleibt abzuwarten, wie sich die Geldpolitik der EZB weiterentwickelt.
Von diesen neueren Entwicklungen aufgrund neuerer geldpolitischer Entscheidungen abgesehen, ist der Fisher-Effekt im Prinzip beobachtbar. Ähnliches gilt auch für internationale Vergleiche.
Hintergrund und Bedeutung
Die Bedeutung des Zinssatzes in der Makroökonomie darf man nicht unterschätzen. Und man sollte sie daher auch oft wiederholen. Gregory Mankiw definiert sie in seinem Makro-Einführungsbuch als „Preise, die die Gegenwart mit der Zukunft verbinden“.
Mindestens drei „Verknüpfungen“ zeigen die Bedeutung dieser makroökonomischen Variablen:
- Interpretation als Preis
- Erwartungen: Verknüpfung der Gegenwart mit der Zukunft
- Analyse: Verknüpfung Geldmarkt und Gütermarkt (vgl. z.B. IS-LM oder AS-AD-Modell)
Die Fisher-Gleichung belegt nun über ihre Herleitung und des folgenden Fisher-Effektes die ersten beiden Punkte.
Entwickelt hat die Gleichung der Ökonom Irving Fisher (1867-1967). Fisher entwickelte ebenfalls die grundlegende Form der Quantitätsgleichung des Geldes. Sie bildet den Ausgangspunkt der Quantitätstheorie des Geldes. Die Gemeinsamkeit der Arbeiten liegt darin, dass ein zentrales Forschungsgebiet von Fisher die Erklärung der Inflation war. Sein Ansatz als „Klassiker“ war, dass Inflation ausschließlich auf eine Veränderung der Geldmenge zurückzuführen sei. Seine verschiedenen Arbeiten sind damit Beiträge, um seine These zu erklären und zu belegen.
Mehr Informationen: Artikel zur Geldmengeninflation
Gegenstand der Quantitätsgleichung und der Fisher-Gleichung ist immer die Beziehung zwischen Inflation und Geldmarkt, wobei in der Fisher-Gleichung der Geldmarkt eine seiner Determinanten, den Zinssatz, dargestellt wird.
Wie oben bereits erwähnt, erklären Quantitätsgleichung und Fisher-Gleichung gemeinsam, wie es zum Fisher-Effekt kommt.
Die Herleitung der Fisher-Gleichung
Die Herleitung der Fisher-Gleichung erfolgt über den Kapitalmarkt. Es geht darum, wie hoch die Rendite einer Person ist, die in Periode 1 seine Ersparnisse zu einem bestimmten Prozentsatz angelegt hat. In der folgenden Periode 2 hebt die Person ihre Ersparnisse und die in diesem Zeitraum aufgelaufenen Zinsen wieder ab. Die Frage ist nun, wie hoch die Zinsen tatsächlich ausgefallen sind.
Deshalb ist die Unterscheidung zwischen Nominal- und Realzinssatz so wichtig. Und inwiefern die Zinsen jetzt die Inflation berücksichtigen.
Nominalzinssatz i: Der Zinssatz, den die Bank zahlt. Er berücksichtigt nicht die Inflationsrate.
Realzinssatz r: Der Zinssatz misst die Zunahme der Kaufkraft. D.h. er berücksichtigt die Inflation. Bzw. ist der Realzinssatz die Differenz zwischen Nominalzinssatz und Inflationsrate
r=i+\pi
Die exakte Formel lautet:
(1+r)=(1+i)/(1+\pi )
Solange r, i und \pi hinreichend klein sind, ist die Gleichung korrekt. Formt man die obige Gleichung nun nach i um, erhält man die Fisher-Gleichung:
i=r+\pi
Wer sich für die Herleitung der exakten Formel interessiert, sei auf den wikipedia-Artikel zur Fisher-Gleichung verwiesen. Auf der Seite wird auch dargestellt, dass die Fisher-Gleichung auf zwei Arten hergeleitet werden kann. Die hier vorgestellte Variante basiert auf dem sogenannten „nominalen Arbitrageargument“. Es geht davon aus, dass nominale Erträge und erwartete nominale Erträge einer realen Investition gleichgesetzt werden. Die zweite Möglichkeit geht von einem „realen Arbitrageargument“ aus. Hier werden erwartete reale Erträge verwendet.
Wirkungen: Geldmarkt, Zinsen und Preise
Wie ausgeführt, ist die Fisher-Gleichung eine wichtige Grundlage, um die Beziehungen zwischen Zinsen und Inflation auf dem Geldmarkt zu erklären.
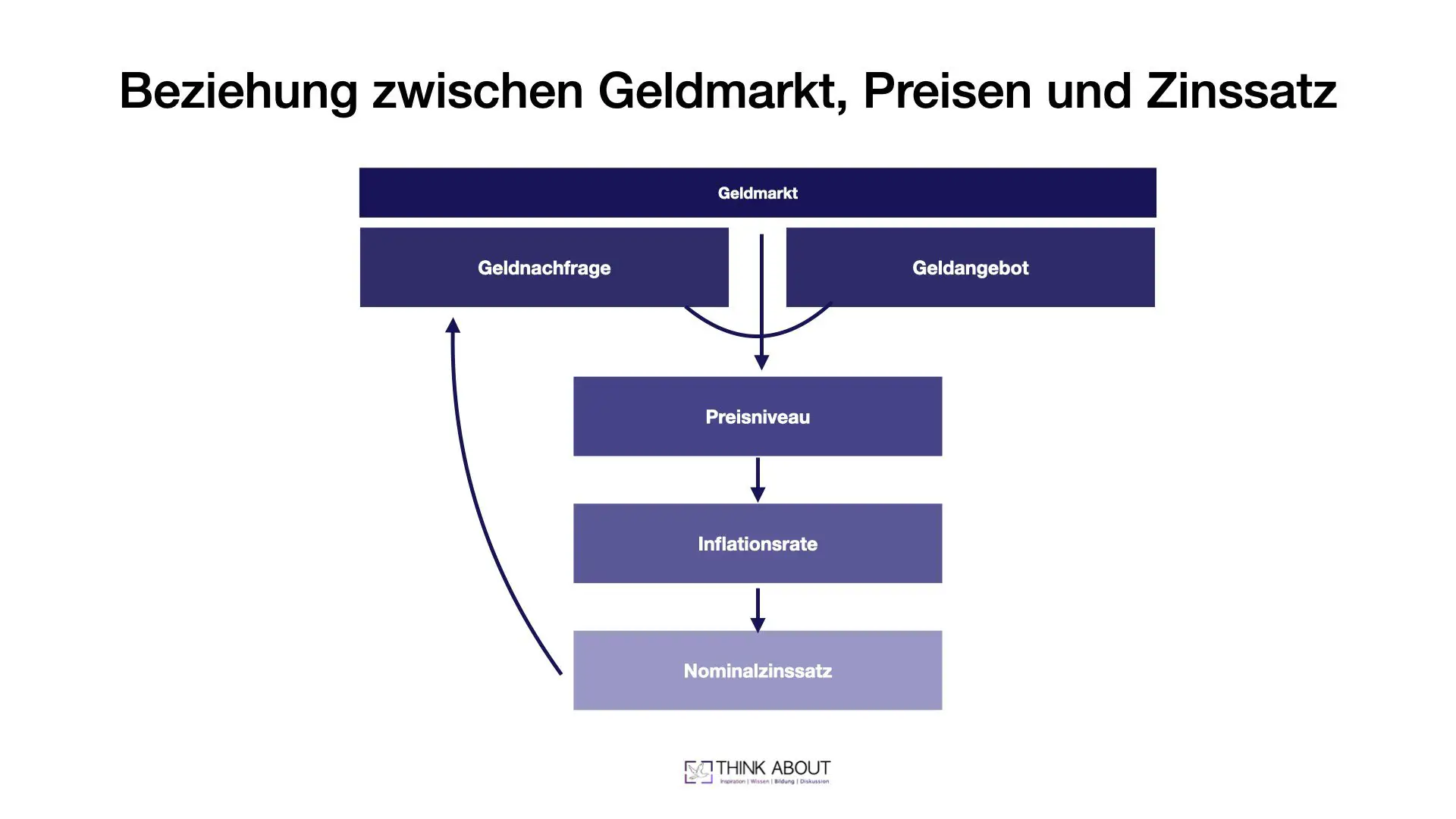
Mit der hier dargestellten Grafik gehen wir ein wenig über das Thema dieses Artikels hinaus. In der Grafik illustrieren wir knapp die Beziehung zwischen Geldmarkt, dem Preisniveau (i.e Inflation) und dem Nominalzinssatz. Wir möchten damit zeigen, wie sich die Fisher-Gleichung in das Gesamtmodell der Klassiker zur Quantitätstheorie des Geldes einfügt.
Wir sehen in der Abbildung als Ausgangspunkt den Geldmarkt. Wie auf jedem Markt gibt es auch hier ein (Geld)Angebot und eine (Geld)Nachfrage. Indem man den Wert der Geldmenge über das Preisniveau interpretiert, folgt das Preisniveau aus dem Geldmarkt. Wir haben diesen Zusammenhang in unserem Artikel zur Quantitätsgleichung des Geldes erklärt: Mehr Informationen findet ihr hier.
Die Veränderungsrate des Preisniveaus ist einfach die Inflationsrate. Die in diesem Artikel erklärte Fisher-Gleichung ist nun die Verbindung der nächsten beiden Schritte in der Abbildung, dass man von der Inflationsrate auf den Nominalzinssatz schließen kann. Der Fisher-Effekt geht noch einen Schritt weiter und zeigt, dass sich beide Faktoren immer im selben Umfang verändern.
Diese Zusammenhänge bilden die (einfache) Quantitätstheorie des Geldes der Klassiker ab. Darüber hinaus gibt es noch einen Zusammenhang zwischen dem Nominalzinssatz und der Geldnachfrage. Der Nominalzinssatz beschreibt über die sogenannte Spekulationskasse die Kosten der Geldhaltung. Insofern kann der Zins auch die Geldnachfrage beeinflussen. Dieser sogenannte „Rückkopplungseffekt“ ist bei den Klassikern vernachlässigt. Die (spätere) Aufteilung der Geldnachfrage in die sogenannte Spekulationskasse (wird durch i bestimmt) und Transaktionskasse (wird durch das Einkommen Y bestimmt) ist ein Verdienst von Keynes.
Anwendung der Fisher-Gleichung
1. Fisher-Effekt
Der Fisher-Effekt kann im Prinzip als Anwendung der Fisher-Gleichung interpretiert werden. Er folgt aus der gemeinsamen Betrachtung der Fisher-Gleichung und der Quantitätsgleichung des Geldes.
Fisher-Effekt: Zwischen Nominalzinssatz und Inflationsrate besteht eine Eins-zu-Einsatz-Beziehung. D.h. beide Variablen steigen im selben Ausmaß.
2. Internationaler Zinszusammenhang bzw. Internationaler Fisher-Effekt
Der internationale Fisher-Effekt wendet die Erkenntnisse im internationalen Kontext an. D.h. neben den inländischen Marktdeterminanten müssen noch die Determinanten und der Markt der Wechselkurse berücksichtigt werden. Und die Kaufkraftparitätentheorie, um die Kaufkraft des Preisniveaus international vergleichen zu können.
Internationaler Fisher-Effekt: Veränderungen in den Wechselkursen am Kassamarkt gehen mit Veränderungen in den nominalen Zinssätzen einher.
Mehr Informationen hierzu in unserem Artikel zum internationalen Zinszusammenhang.
3. Investmentbanken
An den Börsen ist die Beziehung zwischen Inflation und Zinssätzen bekannt. Ein Bestimmungsfaktor des Zinssatzes ist die Nachfrage auf dem Wertpapiermarkt. Genauer: die Wertpapierkurse entwickeln sich entgegengesetzt zu den Zinsen. Mehr Informationen hierzu später in unseren Artikeln zur Geldnachfrage und zur Spekulationskasse.
Aus dieser Beziehung zwischen Fisher-Effekt (Inflation und Zins) und Wertpapierkursen folgt im Investmentbereich ein großes Interesse daran, die Entwicklung von Zinssätzen korrekt vorherzusagen. Deshalb wird in diesem Bereich nicht nur der Aktienmarkt sehr stark beobachtet, sondern auch die Entwicklung der Inflationsrate bzw. Anzeichen für eine Änderung der Geldpolitik oder Inflationsrate. Dies dient dem Ziel, Änderungen des Zinssatzes korrekt abschätzen zu können.
