Die Budgetgerade und Budgetrestriktion beantworten die Frage, was sich ein Konsument von seinem verfügbaren Einkommen leisten kann. Sie stellt einen Hauptteil des mikroökonomischen Standardmodells der Haushaltstheorie dar. In diesem Artikel erfahrt ihr, wie ihr die Budgetgerade zeichnet und berechnet. Außerdem stellen wir euch Anwendungsbeispiele vor und stellen euch Einflussfaktoren und Determinanten vor.
Definition Budgetgerade einfach erklärt
Budgetgerade: Sie zeigt die erreichbaren Konsummöglichkeiten für einen Konsumenten, der sein gesamtes (verfügbares) Einkommen verausgabt. Die Budgetgerade ist die grafische Darstellung der Budgetrestriktion des Konsumenten.
Budgetrestriktion: (auch Budgetbeschränkung) Der Geldbetrag, der dem Konsumenten zum Erwerb von Gütern und Dienstleistungen zur Verfügung steht. Die Konsummöglichkeiten dürfen nicht größer sein als sein (verfügbares) Einkommen.
Die Budgetgerade und die Budgetrestriktion sind Konzepte aus der Mikroökonomie, die den Zusammenhang zwischen den Preisen von Gütern, dem Einkommen und dem verfügbaren Budget eines Individuums beschreiben.
Die Budgetgerade ist eine grafische Darstellung der verschiedenen Kombinationen von Gütern, die ein Individuum mit einem festen Budget und gegebenen Preisen kaufen kann. Sie zeigt die maximalen Mengen der beiden Güter, die das Individuum erwerben kann, unter der Bedingung, dass das gesamte Budget ausgegeben wird. In der Regel wird auf der x-Achse die Menge des einen Gutes und auf der y-Achse die Menge des anderen Gutes dargestellt. Die Steigung der Budgetgerade entspricht dem Verhältnis der Preise der beiden Güter.
Die Budgetrestriktion beschreibt die Einschränkungen, die sich aus dem verfügbaren Budget und den Preisen der Güter ergeben. Sie legt fest, welche Kombinationen von Gütermengen ein Individuum kaufen kann, gegeben das Budget und die Preise. Die Budgetrestriktion wird in der Regel als mathematische Gleichung dargestellt, die das Budget und die Preise der Güter berücksichtigt.
Px * x + Py * y ≤ I,
wobei Px und Py die Preise der Güter, x und y die Mengen der Güter und I das verfügbare Einkommen des Individuums sind.
Die Budgetgerade und die Budgetrestriktion sind eng miteinander verbunden. Die Budgetgerade stellt alle Kombinationen von Gütermengen dar, die das Individuum erwerben kann, während die Budgetrestriktion die Beschränkungen definiert, welche dieser Kombinationen tatsächlich erreichbar sind. Die Lösung des Budgetproblems besteht darin, die optimale Kombination von Gütermengen zu finden, die auf der Budgetgerade liegt und die Präferenzen des Individuums maximiert.
Der Unterschied zwischen Einkommen und Budget liegt in ihrer Bedeutung und Verwendung in der Budgetgleichung:
Einkommen: Das Einkommen bezieht sich auf den Geldbetrag, den eine Person oder ein Haushalt verdient oder zur Verfügung hat. Es repräsentiert die finanziellen Ressourcen, die zur Verfügung stehen, um Güter und Dienstleistungen zu kaufen.
Budget: Das Budget bezieht sich auf den Betrag des Einkommens, der für den Kauf von Gütern und Dienstleistungen verwendet werden soll. Es stellt die Einschränkungen dar, denen eine Person oder ein Haushalt unterliegt, wenn es um den Konsum geht. Das Budget legt fest, wie viel von dem verfügbaren Einkommen für den Kauf verschiedener Güter ausgegeben werden kann.
In der Budgetgleichung werden sowohl das Einkommen als auch das Budget berücksichtigt. Das Einkommen wird als I (für income) dargestellt, während das Budget den Betrag des Einkommens repräsentiert, der für den Konsum verwendet werden kann. Die Budgetgleichung stellt sicher, dass die Gesamtausgaben für Güter und Dienstleistungen das verfügbare Einkommen nicht übersteigen.
Hintergrund: Bedeutung der Budgetgerade in der Haushaltstheorie
Die Haushaltstheorie beschäftigt sich mit der Frage, wie ein Individuum seine begrenzten Ressourcen (Budget) optimal nutzen kann, um seine Bedürfnisse zu befriedigen. Das Individuum steht vor der Entscheidung, wie es sein verfügbares Einkommen auf verschiedene Güter aufteilt, um seinen Nutzen zu maximieren. Die Haushaltstheorie basiert auf der Annahme, dass das Individuum bestimmte Präferenzen hat, die sich in einer Nutzenfunktion widerspiegeln.
Die Budgetrestriktion ist eine zentrale Komponente der Haushaltstheorie. Sie beschreibt die finanziellen Einschränkungen, denen das Individuum unterliegt. Das Individuum kann nur Gütermengen kaufen, für die die Ausgaben innerhalb des verfügbaren Budgets liegen. Die Budgetrestriktion ist durch eine mathematische Gleichung oder Ungleichung dargestellt, die das verfügbare Budget, die Preise der Güter und die gekauften Mengen berücksichtigt.
Die Budgetgerade ist eine grafische Darstellung der Budgetrestriktion. Sie zeigt alle Kombinationen von Gütermengen, die ein Individuum mit einem gegebenen Budget und den Preisen der Güter kaufen kann. Die Budgetgerade wird oft in einem zweidimensionalen Diagramm dargestellt, wobei auf der x-Achse die Menge eines Gutes und auf der y-Achse die Menge eines anderen Gutes liegt. Die Steigung der Budgetgerade entspricht dem Verhältnis der Preise der Güter.
Der Zusammenhang zwischen der Budgetgerade, der Budgetrestriktion und der Haushaltstheorie besteht darin, dass die Budgetgerade die möglichen Kombinationen von Gütermengen darstellt, die das Individuum unter Beachtung der Budgetrestriktion erreichen kann. Das Individuum versucht, eine Kombination von Gütermengen zu wählen, die auf der Budgetgerade liegt und seine Präferenzen maximiert. Die Haushaltstheorie analysiert die Entscheidungsfindung des Individuums unter Berücksichtigung dieser Restriktionen und versucht, vorherzusagen, wie das Individuum seine Ressourcen optimal alloziert, um seinen Nutzen zu maximieren.
Herleitung der Budgetrestriktion
Die Budgetrestriktion wird hergeleitet, indem man das verfügbare Budget eines Individuums und die Preise der Güter berücksichtigt.
Angenommen, ein Individuum hat ein bestimmtes Budget I und möchte zwei Güter x und y kaufen. Die Preise der Güter werden mit Px und Py bezeichnet. Das Individuum entscheidet, wie viel von jedem Gut es kaufen möchte, und die Kosten für den Kauf dieser Gütermengen dürfen das verfügbare Budget nicht überschreiten.
Die Kosten für das Gut x sind gegeben durch den Preis Px multipliziert mit der Menge x, also Px * x. Entsprechend sind die Kosten für das Gut y gegeben durch den Preis Py multipliziert mit der Menge y, also Py * y.
Die Budgetrestriktion besagt nun, dass die Gesamtkosten für den Kauf der Gütermengen x und y das verfügbare Budget I nicht überschreiten dürfen. Mathematisch ausgedrückt ergibt sich die Budgetrestriktion folgendermaßen:
Px * x + Py * y ≤ I
Diese Ungleichung stellt sicher, dass die Ausgaben für die Gütermengen x und y zusammenaddiert das Budget nicht übersteigen. Die Budgetrestriktion kann auch als Gleichung dargestellt werden, wenn das Individuum sein gesamtes Budget genau ausgeben möchte:
Px * x + Py * y = I
Hierbei sind Px * x und Py * y die Ausgaben für die Gütermengen x und y, und I ist das verfügbare Budget.
Die Budgetrestriktion stellt somit sicher, dass ein Individuum nur Kombinationen von Gütermengen erwerben kann, für die die Gesamtausgaben innerhalb des verfügbaren Budgets liegen.
Zeichnen der Budgetgerade
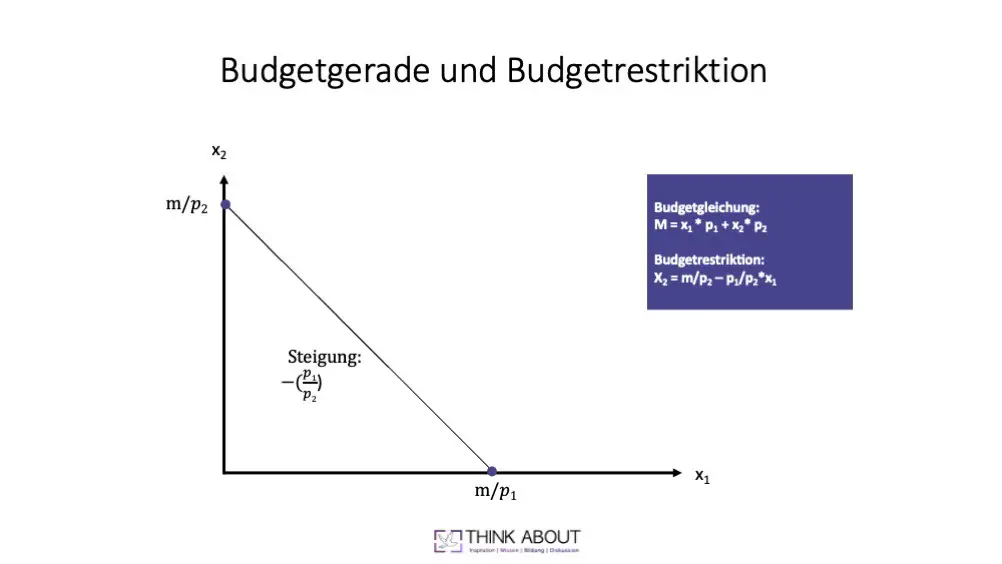
Um die Budgetrestriktion wie in der Abbildung aufzustellen und die Budgetgerade zu zeichnen, führe diese Schritte aus:
- 1Stelle die Budgetgleichung auf: Die Budgetgleichung wird in der Regel durch die lineare Gleichung P1 * x1 + P2 * x2 = m dargestellt. Hierbei steht P1 für den Preis des Gutes x1, P2 für den Preis des Gutes x2, x1 und x2 für die Mengen der Güter und m für das verfügbare Budget.
- 2Löse die Budgetgleichung für eine Variable: Setze eine der Variablen (x1 oder x2) auf null und löse die Gleichung für die andere Variable. Wiederhole diesen Schritt, um verschiedene Kombinationen von Gütermengen zu erhalten. Normalerweise wählt man einige sinnvolle Werte für eine der Variablen und berechnet dann die Werte der anderen Variable. Beispielsweise kann man den Wert von x1 auf 0 setzen und x2 berechnen. Dann kann man den Wert von x2 auf 0 setzen und x1 berechnen. So erhält man auch bereits die Achsenschnittpunkte.
- 3Zeichne die Budgetgerade: Nimm die gefundenen Kombinationen von Gütermengen und trage sie in ein Koordinatensystem ein, wobei x1 und x2 die Achsen darstellen. Verbinde die Punkte miteinander, um die Budgetgerade zu zeichnen. Beachte hierbei, dass die Steigung der Budgetgerade dem Verhältnis der Preise der Güter entspricht.
- 4Optional: Wenn du eine Budgetungleichung verwendest, markiere den Bereich unterhalb der Budgetgerade, der die erreichbaren Güterkombinationen darstellt.
Die Budgetgerade wird normalerweise als gerade Linie dargestellt. Ihre genaue Position und Steigung hängen von den spezifischen Werten des Budgets und der Preise der Güter ab. Durch die Veränderung des Budgets oder der Preise können sich die Position und Form der Budgetgerade ändern.
Es ist wichtig zu beachten, dass die genaue Form der Budgetgerade von den spezifischen Werten des Budgets und der Preise der Güter abhängt. Indem ihr verschiedene Werte für das Budget und die Preise verwendet, könnt ih verschiedene Budgetgeraden zeichnen, um den Zusammenhang zwischen den Gütermengen und den finanziellen Einschränkungen zu untersuchen.
Einflussfaktoren der Form der Budgetgerade
Die Form der Budgetgleichung kann sich aus verschiedenen Gründen ändern. Hier sind einige Beispiele:
- Veränderung der Anzahl der betrachteten Güter: Wenn sich die Anzahl der betrachteten Güter ändert, ändert sich auch die Form der Budgetgleichung. Wenn beispielsweise ein weiteres Gut in die Analyse einbezogen wird, wird die Budgetgleichung um einen weiteren Term erweitert, der die Ausgaben für dieses Gut berücksichtigt.
- Inklusion von Steuern oder Subventionen: Wenn Steuern oder Subventionen auf die Preise der Güter wirken, werden sie in der Budgetgleichung berücksichtigt und können zu zusätzlichen Termen führen. Steuern erhöhen die Kosten für den Kauf von Gütern, während Subventionen die Kosten senken. Diese Änderungen wirken sich auf die Form der Budgetgleichung aus.
- Berücksichtigung von Preisnachlässen oder Rabatten: Wenn Preisnachlässe oder Rabatte auf bestimmte Güter gewährt werden, können sie die Form der Budgetgleichung beeinflussen. Die Kosten für den Kauf dieser Güter werden reduziert, was zu einer Änderung der Preise und somit zu einer Anpassung der Budgetgleichung führt.
- Veränderung der Präferenzen oder Bedürfnisse: Wenn sich die Präferenzen oder Bedürfnisse einer Person ändern, kann dies Auswirkungen auf die Form der Budgetgleichung haben. Wenn zum Beispiel eine Person ein größeres Bedürfnis nach einem bestimmten Gut hat, kann dies zu einer Umverteilung des Budgets führen und somit zu einer Anpassung der Gewichtungen oder Koeffizienten in der Budgetgleichung.
Diese Beispiele verdeutlichen, dass Änderungen in der Form der Budgetgleichung durch verschiedene Faktoren bedingt sein können, darunter die betrachteten Güter, externe Einflüsse wie Steuern und Subventionen, Preisnachlässe oder Rabatte sowie Veränderungen der Präferenzen oder Bedürfnisse.
Determinanten der Budgetgerade und Budgetrestriktion
Das Einkommen und die Güterpreise beeinflussen die Lage der Budgetgerade. In der Regel analysiert man, wann sich die Budgetgerade bei Einkommensänderungen verschiebt und wie sie sich bei Preisänderungen dreht. Bereits fortgeschritten ist die Analyse von Mengenrabatten, die zu einem Knick der Budgetgerade führen.
Nachfolgend stellen wir diese grundlegenden Beispiele zur Analyse der Budgetgerade anhand von Abbildungen vor. Um deutlich zu machen, dass die erworbene Gütermenge sowohl vom Einkommen als auch vom Güterpreis abhängt, halten wir die Grafiken allgemein und verwenden hier kein Zahlenbeispiel.
Hinweis: Je nach Lehrbuch unterscheiden sich die Bezeichnungen für die Modellbestandteile. In den Grafiken haben wir für Einkommen den Buchstaben m (money) gewählt. Weiter oben im Artikel wurde für das Einkommen der Buchstabe I (income) verwendet. Beide Bezeichnungen sind richtig und weit verbreitet.
Verschiebung der Budgetgerade: Einkommensänderung
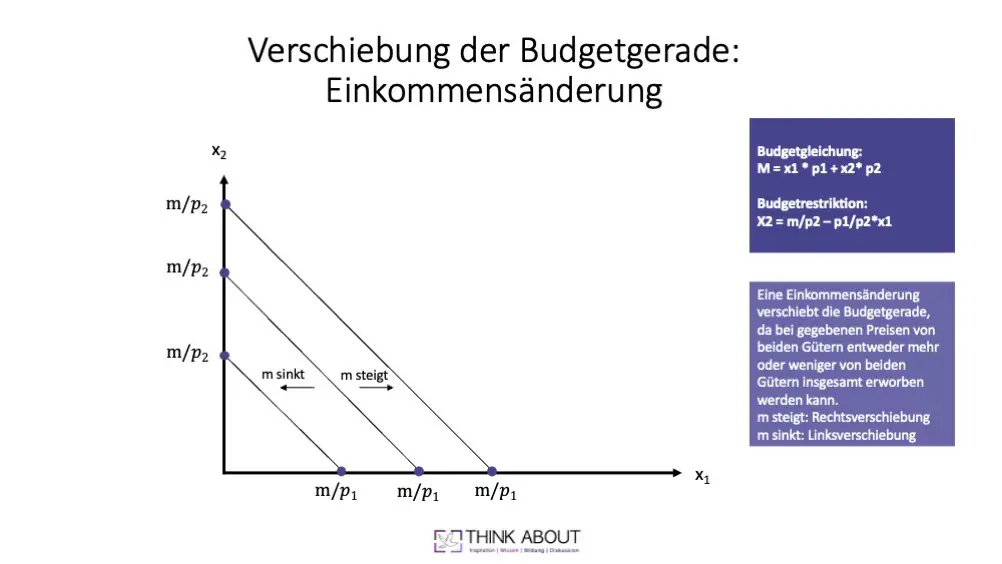
Bei dem (verfügbaren) Einkommen bzw. dem Budget handelt es sich um eine sogenannte exogene Größe. D.h. die Höhe des Einkommens ist vorgegeben. Nur „äußere“ Umstände können es beeinflussen, die nichts mit den Variablen im Modell zu tun haben. Deshalb verschiebt sich die Budgetgerade bei einer Einkommensveränderung. Erhöht sich das Einkommen, kann der Konsument bei unveränderten Preisen ceteris paribus eine größere Menge der beiden Güter erwerben. Das Gegenteil tritt bei einer Verringerung des Einkommens ein.
Es gilt:
Erhöhung des Einkommens: (Parallele) Verschiebung nach rechts außen der Budgetgerade
Reduzierung des Einkommens: (Parallele) Verschiebung nach innen links der Budgetgerade.
Drehung der Budgetgerade: Preisänderung
Im Gegensatz zum Einkommen bilden Preise endogene Größen in dem Modell der Konsumentscheidung. Grundsätzlich gilt zwar, dass z.B. eine Preissteigerung dazu führt, dass ein Konsument weniger von dem Gut erwirbt. Aber wie wirkt sich dies auf das andere Gut aus? Je nachdem, ob das Gut z.B. komplementär oder substitutiv ist, ruft die Preisänderung unterschiedliche Reaktionen hervor. Deshalb sind Preise endogene Größen.
1. Preisänderung Gut 1
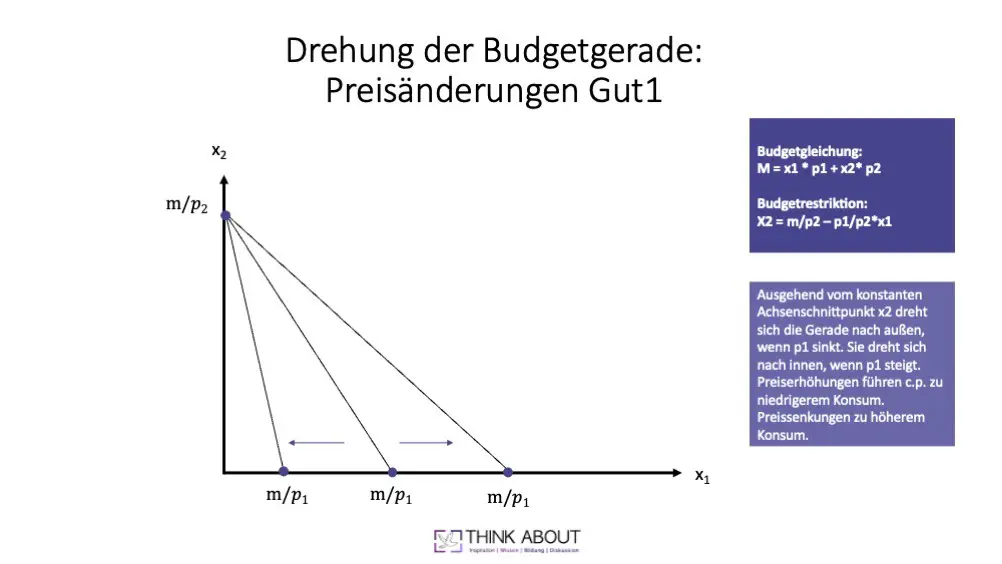
Die Grafik bildet die Auswirkungen von Preisänderungen bei Gut 1 ab. Das Einkommen und der Preis von Gut 2 bleiben konstant.
Damit bleibt auch der Achsenschnittpunkt von Gut 2 unverändert. Eine Preisänderung von Gut 1 führt damit ceteris paribus zu einer Drehung der Budgetgerade.
Steigt der Preis, dreht sich die Gerade nach innen. Sinkt der Preis, dreht sie sich nach außen.
2. Preisänderung Gut 2
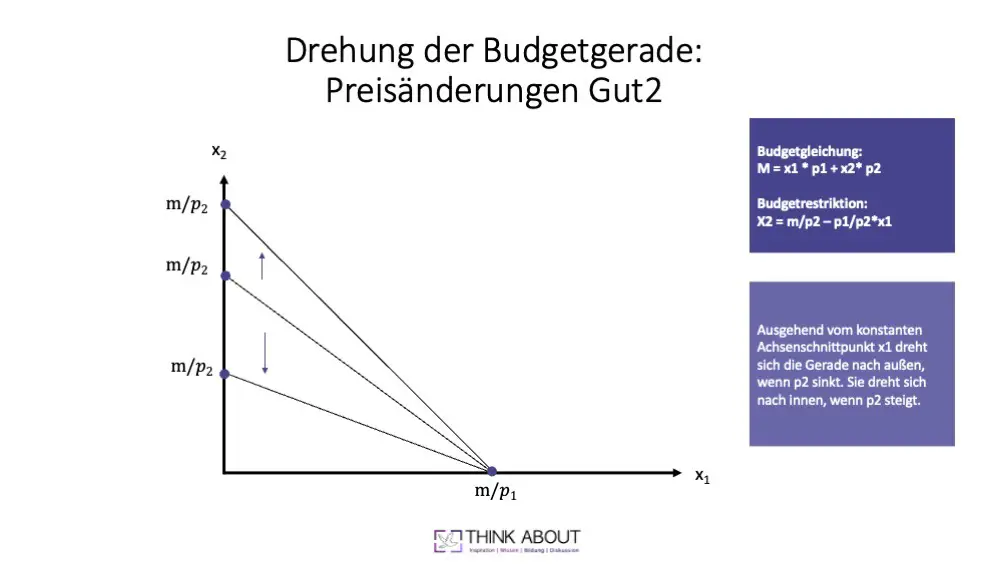
Hier seht ihr den Fall, wenn sich der Preis von Gut 2 ceteris paribus ändert.
Das Prinzip ist dasselbe wie bei Gut 1. Nur „die Sicht“ ist nun anders. Ausgehend vom unveränderten Achsenschnittpunkt von Gut 1, dreht sich die Budgetgerade nach innen, wenn der Preis von Gut 2 steigt. Denn bei gleichbleibendem Einkommen m, kann der Konsument jetzt weniger Einheiten von Gut erwerben. Sinkt der Preis, dreht sich die Kurve nach außen.
3. Gemeinsame Preisänderung Gut 1 und Gut 2
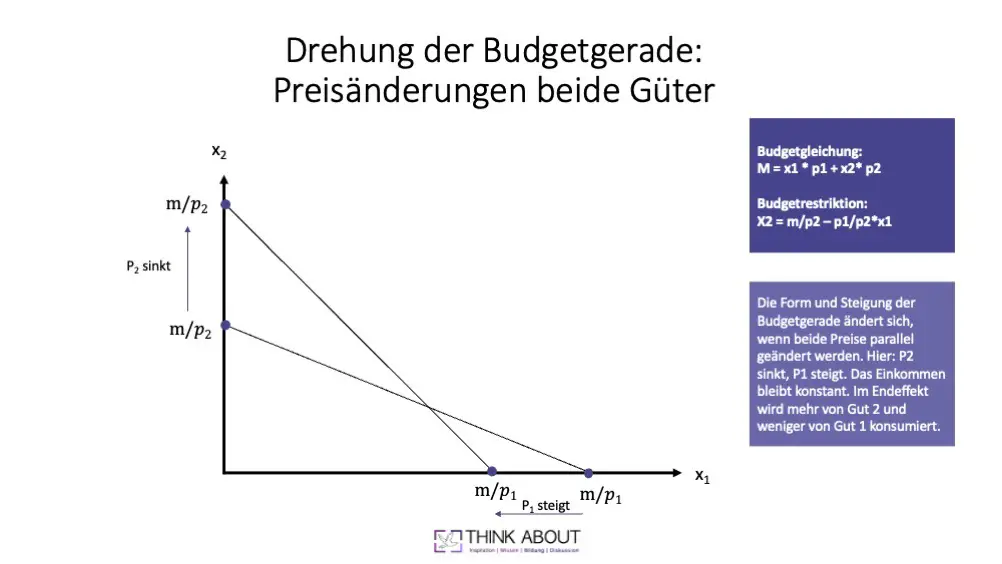
Abschließend haben wir den Fall, wenn sich beide Preise von Gut 1 und Gut 2 ändern. Wie die Budgetgerade abschließend aussieht, hängt vom Preisverhältnis der beiden Güter zueinander ab.
In der Grafik ist der Preis von Gut 2 gefallen und der Preis von Gut 1 gestiegen. Entsprechend würde der Konsument nun bei gleichbleibendem Einkommen mehr Einheiten von Gut 2 erwerben und weniger Einheiten von Gut 1. Aufgrund der parallelen Preisänderungen ändert sich das Preisverhältnis und damit auch der Verlauf bzw. die Steigung der Budgetgerade.
Veränderung der Budgetrestriktion: Rationierung und Mengenrabatt
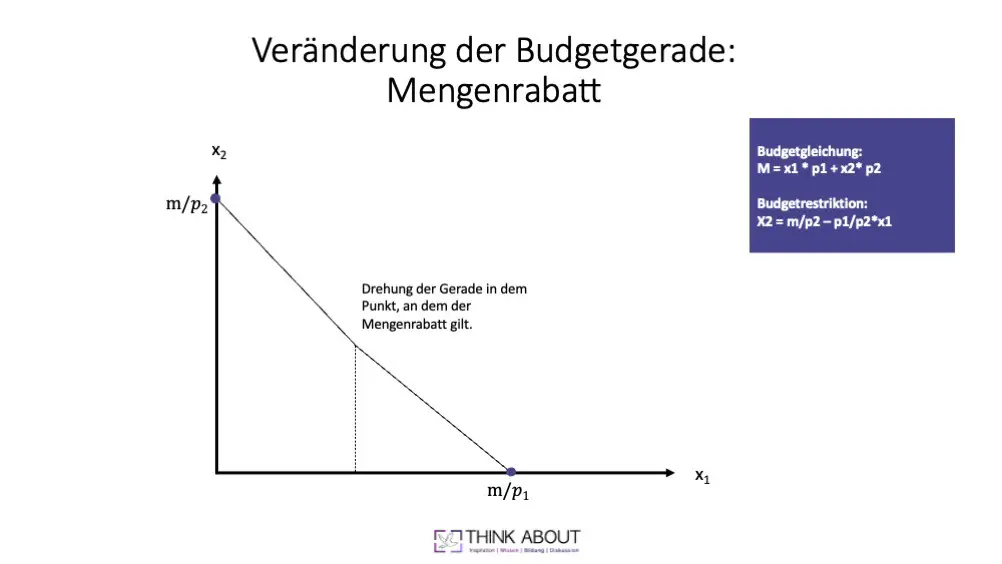
Im Abschnitt zu den Determinanten der Gestalt der Budgetgeraden hatten wir auch Rabatte aufgeführt. Wir waren da aber von konstanten Rabatten ausgegangen. Konkrete Auswirkungen auf die Gestalt der Budgetgerade haben z.B. Mengenrabatte. Dieser Fall ist für einen nicht näher bestimmte Situation dargestellt.
Nehmen wir an, für die ersten 10 Einheiten eines Gutes beträgt der Preis 5 Euro. Auf dieser Grundlage teilt der Konsument sein Einkommen auf und es ergibt sich die dargestellte Form der Budgetgerade. Aber Einheit 11 des Gutes erhält der Konsument jetzt aber einen Rabatt, woraus letztlich für ihn ein Preis von 4 Euro resultiert.
Bei gegebenem Einkommen kann der Konsument jetzt ab Einheit 11 (noch) mehr von dem Gut erwerben. Bei der Budgetgerade macht sich dieser Mengenrabatt durch einen leichten „Knick“ an diesem Punkt bemerkbar. Im Prinzip handelt es sich hierbei um eine Drehung der Budgetgerade in Punkt 11 aufgrund einer (impliziten) Preisänderung.
Beispiel zur Aufstellung und Zeichnung der Budgetgeraden
Beispiel Budgetgerade und Budgetrestriktion
Nehmen wir an, ein Konsument hat einen Geldbetrag von 1.000 Euro zur Verfügung, um für die nächste Party Getränke und Essen zu kaufen. Diese 1.000 Euro stellen damit seine Budgetbeschränkung dar. Unser Konsument entschließt sich Döner und Cola zu kaufen. Eine Dose Cola kostet 2 Euro und ein Döner 10 Euro. Die Frage ist jetzt, wie der Konsument die 1.000 Euro optimal auf die Kombination Cola und Döner bei den gegebenen Preisen aufteilt.
In der Tabelle seht ihr verschiedene Kombinationsmöglichkeiten abgebildet.
Alle Cola-Döner-Kombinationen, bei denen die Gesamtausgaben 1.000 Euro betragen liegen auf der Budgetgerade. Eine Kombination, mit Ausgaben größer 1.000 Euro kann unser Konsument nicht realisieren.
In der Grafik haben wir einige Kombination beispielhaft abgebildet. Um die Budgetgerade zu zeichnen, benötigt ihr die die beiden Achsenschnittpunkte. D.h. bei Ausgaben von 1.000 Euro ist jeweils der Kauf von Dönern oder Cola gleich null.
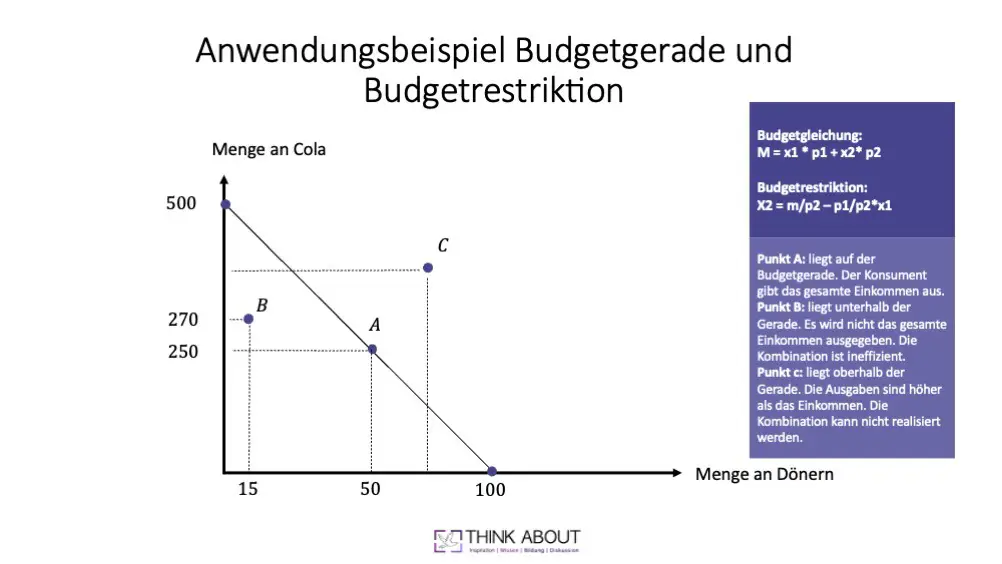
Abgebildet haben wir mit Punkt C außerdem die Kombination, bei der die Ausgaben größer 1.000 Euro sind. Und eine Kombination mit Ausgaben kleiner 1.000 Euro in Punkt B. Dieser Punkt liegt links bzw. unterhalb der Budgetgerade. Er zeigt damit, dass das verfügbare Einkommen nicht optimal bzw. effizient auf die Cola-Döner-Konsummöglichkeiten aufgeteilt wurde.
Ausblick: Die optimale Konsumentscheidung: Nutzen und Budgetgerade
Die bisherigen Ausführungen zur Budgetgerade waren eher „mechanischer“ Natur. Folgt man dem Einführungsbuch zur VWL von Mankiw adressiert die Haushaltstheorie zur Konsumentscheidung des Verbrauchers drei Fragen:
- Was kann der Konsument sich leisten?
- Was will der Konsument?
- Was wählt der Konsument?
Die Budgetgerade beantwortet mit der Budgetrestriktion die erste Frage. Die zweite Frage beantworten die Konzepte, wie Präferenzen und Nutzen, Indifferenzkurven und die Grenzrate der Substitution.
Budgetgerade und Indifferenzkurve beantworten in ihrem Schnittpunkt schließlich die dritte Frage. Der Schnittpunkt bringt die monetären Möglichkeiten des Konsumenten mit seinen Präferenzen und seinem Nutzen aus dem Konsum zusammen.
Ohne bereits auf die optimale Konsumentscheidung einzugehen, möchten wir euch anhand der folgenden Tabelle einen Ausblick auf die weitere Anwendung der Budgetgerade geben.
Beispiel Nutzenoptimierung und Budgetgerade
Die Tabelle folgt unserem Döner-Cola-Beispiel. Sie zeigt fünf Konsumkombination, die auf der Budgetgerade liegen. Außerdem haben wir die Tabelle um Werte zum Nutzen ergänzt, den der Konsument aus dem Erwerb der jeweiligen Güter zieht. Mit steigendem Konsum steigt auch der jeweilige Nutzen. Allerdings ist der Nutzenzuwachs abnehmen (Gesetz vom abnehmenden Grenznutzen).
Die optimale Konsumentscheidung des Konsumenten stellt nun diejenige Auswahl dar, wo auf der Budgetgerade der Gesamtnutzen am höchsten ausfällt.
Hierbei handelt es sich um das Güterbündel C. Der Konsument erhält hier für 1.000 Euro 250 Cola Flaschen und 50 Döner. Resultierende Gesamtnutzen beträgt 59 Einheiten und fällt von allen angegebenen Güterbündeln am höchsten aus.
Andere Anwendungsbereiche des Konzeptes der Budgetgerade
Das Konzept der Budgetgerade hat Anwendungsbereiche in verschiedenen Bereichen, in denen Budgetbeschränkungen und Preise eine Rolle spielen. Hier sind einige Beispiele:
Die Anwendungsbereiche der Budgetgerade sind vielfältig und reichen von der persönlichen Finanzplanung bis hin zur Makroökonomie. Sie dient als nützliches Werkzeug, um Budgetbeschränkungen zu berücksichtigen und fundierte Entscheidungen zu treffen. Aber auch außerhalb der VWL könnt ihr das Konzept übertragen und verwenden.
fAQ: Häufige Fragen zur Budgetgerade und Budgetrestriktion
Die Budgetgleichung ist eine mathematische Gleichung, die das verfügbare Budget (I) eines Individuums oder Haushalts zur Verfügung stellt. Sie stellt die finanzielle Beschränkung dar, welche die Ausgaben für den Kauf von Gütern begrenzt. In der Regel wird die Budgetgleichung durch die lineare Gleichung Px * x + Py * y = I repräsentiert, wobei Px und Py die Preise der beiden betrachteten Güter sind und x und y die Mengen der Güter darstellen.
Die Steigung der Budgetgeraden wird berechnet, indem man das Verhältnis der Preise der beiden betrachteten Güter (Px und Py) verwendet. Die Steigung wird als negative Koeffizienten Relation dargestellt, also -Px/Py. Dies bedeutet, dass eine Einheit des Gutes x im Austausch gegen die Steigungseinheit des Gutes y aufgegeben wird. Die Steigung gibt an, wie viel von Gut y für eine zusätzliche Einheit von Gut x aufgegeben werden muss, um das Budget nicht zu überschreiten.
Die Budgetgerade verschiebt sich, wenn sich die Bedingungen ändern, die die Budgetrestriktion beeinflussen. Dies kann geschehen bei Änderungen des Einkommens bzw. der Menge des Budgets. Eine Erhöhung des Einkommens oder des Budgets verschiebt die Budgetgerade nach außen, während eine Verringerung sie nach innen verschiebt.
Die Budgetgerade dreht sich, wenn sich das Verhältnis der Preise der betrachteten Güter ändert. Wenn sich das Preisverhältnis erhöht, wird die Budgetgerade steiler, was bedeutet, dass der Konsument mehr von Gut y opfern muss, um mehr von Gut x zu konsumieren. Wenn sich das Preisverhältnis verringert, wird die Budgetgerade flacher, und der Konsument muss weniger von Gut y opfern, um mehr von Gut x zu konsumieren.
