Der Grenznutzen entspricht dem Zusatznutzen durch den Konsum einer weiteren Einheit eines Gutes. In diesem Artikel erklären wir euch Definition, Berechnung und Darstellung. Außerdem gehen wir auf den abnehmenden Grenznutzen ein, sowie auf den Zusammenhang mit dem ersten und zweiten Gossenschen Gesetz.
Definition Grenznutzen einfach erklärt
Grenznutzen: Der zusätzliche Nutzen, den der Konsum einer zusätzlichen Einheit eines Gutes stiftet.
Der Grenznutzen stellt den Nutzenzuwachs dar, den ein Konsument eine weitere Einheit eines Gutes konsumiert. Allgemein gilt, dass dieser Nutzenzuwachs abnimmt, wenn sich die konsumierte Menge erhöht. Ist der Grenznutzen gleich null, ist der Sättigungspunkt eingetreten. Er kann auch negativ sein, wenn Übersättigung eintritt bzw. der Konsum eines Gutes schadet.
Diese etwas sperrige Formulierung ist mit Hilfe eines Beispiels leicht verständlich: Angenommen, du hast im Sommer Durst und trinkst deshalb ein Glas eisgekühlte Cola. Aus diesem Glas Cola erzielst du einen hohen Nutzen, denn dein erster großer Durst ist gestillt. Anschließend trinkst du noch ein zweites Glas Cola. Da dein größter Durst gelöscht ist, nimmst du dir jetzt auch mehr Zeit für den Konsum des Glases. Du erzielst zwar immer noch Nutzen aus dem Konsum von Cola. Allerdings fällt der zusätzliche Nutzen, den du aus dem zweiten Glas erhältst, jetzt geringer aus. Wenn du keinen Durst mehr hast, ist dein Bedarf gesättigt und der Grenznutzen gleich null. Trinkst du jetzt aber trotzdem noch mehrere Gläser Cola, kann es sein, dass dir irgendwann schlecht wird. In diesem Fall wäre dein Grenznutzen negativ.
Das Beispiel deutet bereits darauf hin, dass der Grenznutzen bzw. der abnehmende Grenznutzen aus der Nutzenfunktion eines Konsumenten und den darin enthaltenen Annahmen abgeleitet ist. Mathematisch und grafisch resultiert der Grenznutzen bzw. die Grenznutzenkurve aus der Nutzenfunktion. Man berechnet sie über die erste Ableitung der Nutzenfunktion.
Die Annahme des abnehmenden Grenznutzens bezeichnet man auch als erstes Gossensches Gesetz. Das Konzept ist ein zentraler Bestandteil der Haushaltstheorie in der Mikroökonomie und beschreibt damit die Entscheidungsfindung auf der Nachfrageseite. Demgegenüber steht die Angebotsseite mit der Unternehmenstheorie mit entsprechenden Konzepten.
Abgrenzungen
Das Prinzip der Grenzeinheit ist Kern des Ansatzes der Neoklassik in der VWL. Man findet deshalb dieses allgemeine Analyseprinzip über die entsprechenden Ausdrücke sowohl auf der Nachfrageseite als auch der Angebotsseite. Wir möchten dir deshalb kurz die relevanten Begriffe auf den beiden Marktseiten definieren. Dadurch merkst du schnell, dass es im Prinzip egal ist, ob du dich in der Haushaltstheorie oder in der Produktionstheorie der Mikroökonomie befindest. Das zugrundeliegende Prinzip ist immer dasselbe.
Haushalte: Gesamtnutzen vs. Grenznutzen und abnehmender Grenznutzen
Bei den Haushalten ist es sinnvoll, zur Veranschaulichung zwischen dem Gesamtnutzen und dem Grenznutzen zu unterscheiden. Hierdurch sehr ihr noch einmal, was seinen Kern ausmacht:
Gesamtnutzen: Die Bedürfnisbefriedigung, die ein Konsument durch den Konsum eines Gutes erlangt.
Grenznutzen: Der zusätzliche Nutzen, den der Konsum einer zusätzlichen Einheit eines Gutes stiftet.
Unternehmen: Grenznutzen vs. Grenzerlös und Grenzkosten
Während ihr euch bei den Haushalten hauptsächlich mit der Nutzenmaximierung und dementsprechend dem Grenznutzen beschäftigt, stehen bei den Unternehmen dagegen zwei Parameter im Mittelpunkt: Erlöse und Kosten. Das Unternehmen stellt Güter her und verkauft sie anschließend. Durch den Verkauf erzielt er Erlöse bzw. Umsatz. Und für die Produktion entstanden ihm Kosten.
Das Unternehmen interessiert sich demnach dafür, erstens seinen Umsatz bzw. Erlös zu maximieren. Andererseits hat es aber auch ein starkes Interesse daran, seine entstehenden Produktionskosten möglichst gering zu halten. Im Endeffekt geht durch die Berücksichtigung beider Faktoren darum, die Produktion effizient zu gestalten. Für die Analysen sind deshalb die Begriffe Grenzerlös bzw. Grenzumsatz und Grenzkosten von Bedeutung:
Grenzerlös: Die Veränderung des Gesamterlöses durch den Verkauf einer zusätzlichen Einheit des Gutes.
Grenzkosten: Betrag, um den die Gesamtkosten der Produktion einer zusätzlichen Gütereinheit ansteigen.
Historischer Hintergrund: Grenznutzenschule, Marshall, Pareto, Adam Smith und Gossen
Die Grenznutzenschule ist eine in verschiedenen europäischen Ländern ungefähr gleichzeitig entstandene Theorie, in der die Analyse des Nutzens in der Volkswirtschaft in den Mittelpunkt gestellt wurde. Hierfür wurde das „Grenzprinzip“ (marginal) auf die Nutzenanalyse angewendet. Dieses Konzept war damals so revolutionär, dass man von einer „marginalistischen Revolution“ sprach. Die Vertreter dieses Theorieansatzes begründeten die neoklassische Theorie in der VWL.
Für das Verständnis des Grenznutzenansatzes ist es sinnvoll, wenn man sich in Erinnerung ruft, dass es in der VWL auch immer um Entscheidungen geht. Und damit einhergehend zudem um die Bewertung dieser Entscheidungen. Den Grenznutzen kann man im Extrem verstehen, als denjenigen Nutzen, den mir die letzte mir zur Verfügung stehende Einheit des Gutes gibt, um meinen Bedarf zu stillen. Denn nur wenn mein Bedarf vollständig gedeckt ist, habe ich den größtmöglichen Nutzen erhalten.
Bei der Grenznutzentheorie der Neoklassiker handelt es sich um eine subjektive Wertlehre. D. h. es fließen der individuelle Nutzen und die Kosten in die Entscheidung ein. Dieses Prinzip gilt für alle Bereich in der VWL. Also nicht nur für die Nachfrage, sondern auch für das Angebot. Entsprechend gibt es auch die vorher abgegrenzten Begriffe Grenzerlös etc.
Die Gossenschen Gesetze: Welche Bedeutung hat der Grenznutzen in der VWL?
Das erste Gossensche Gesetz: Dieses Gesetz ist eine verbale Formulierung des Prinzips des abnehmenden Grenznutzens. Man bezeichnet es auch als Gesetz vom abnehmenden Grenznutzen oder Sättigungsgesetz.
Das erste Gossensche Gesetz: Dieses Gesetz ist eine verbale Formulierung des Prinzips des abnehmenden Grenznutzens. Man bezeichnet es auch als Gesetz vom abnehmenden Grenznutzen oder Sättigungsgesetz.
„Die Größe des Genusses nimmt, wenn mit der Bereitung des Genusses ununterbrochen fortgefahren wird, fortwährend ab, bis zuletzt Sättigung eintritt“.
Das zweite Gossensche Gesetz: Dieses Gesetz verteilt in seiner ursprünglichen Formulierung das verfügbare Einkommen eines Konsumenten bzw. Haushaltes dergestalt auf die Befriedigung seiner Bedürfnisse (Erwerb von Konsumgütern), dass er den höchsten Nutzen erzielt.
Demnach befindet sich ein Haushalt dann in seinem Optimum, wenn die Grenznutzen für alle konsumierten Güter, geteilt durch den Preis, übereinstimmen. Wäre dies nicht Fall, wäre es dem Haushalt möglich, durch eine Umstrukturierung seiner Konsumgüter seinen Nutzen zu erhöhen oder denselben Nutzen zu niedrigeren Kosten zu erzielen.
Das zweite Gossensche Gesetz ist weniger streng als das erste Gesetz in Bezug auf die Annahmen der Eigenschaften der Nutzenfunktion formuliert. Während Gossen selbst von einer kardinalen Nutzenmessung ausging, gilt das zweite Gossensche Gesetz sowohl für kardinale als auch ordinale Nutzenmessung.
In der Anwendung bedeutet dies, dass bei der Interpretation und grafischen Darstellung nur noch das Vorzeichen des Wertes relevant ist, nicht aber mehr die Steigung.
In der Haushaltstheorie ist das zweite Gossensche gleichbedeutend mit dem „Beweis“, dass im Haushaltsoptimum das Verhältnis der Grenzrate der Substitution zweier Güter bzw. die Steigung der Indifferenzkurve identisch ist mit ihrem Preisverhältnis.
Mit welcher Formel berechnet man den Grenznutzen?
Nehmen wir an, wir haben die folgende Cobb-Douglas-Nutzenfunktion vorliegen:
U(x,y)=x^{0,5}*y^{0,5}
X ist die Menge von Sprite in Gläsern
Y ist die Menge von Cola in Gläsern
Wir möchten jetzt Grenznutzen von Cola bzw. y berechnen. Die konsumierte Menge von Sprite bzw. die Anzahl der Gläser ist auf x = 4 festgelegt. Wir setzen diesen Wert in die Nutzenfunktion ein und bekommen folgenden Ausdruck:
U(\bar{x} , y)= 4^{0,5}* y^{0,5}=2*y^{0,5}
Den Grenznutzen für Cola berechnet ihr, indem ihr die Nutzenfunktion nach y ableitet:
\frac{\partial U(\bar{x},y)}{\partial y} = 1 * y^{-0,5}
Wertmäßig erhaltet ihr den Grenznutzen für den Konsum von einer bestimmten Menge Cola, wenn ihr entsprechende Werte von y in die Funktion einsetzt. Z.B. trinkst du 4 Gläser Cola. Diesen Wert setzt du in die Funktion (y=4) und löst auf:
4^{-0,5}=\frac{1}{\sqrt{4}}=0,5
Der Grenznutzen ist in diesem Fall 0,5. Er ist abnehmend. Dies zeigt ihr, über die zweite Ableitung der Funktion y hoch -0,5:
f ''(y)=-\frac{1}{2y^{3/2}}<0
Die zweite Ableitung ist kleiner Null. Damit habt ihr auch mathematisch gezeigt, dass es sich um einen abnehmenden Grenznutzen handelt.
Grafische Darstellung des Grenznutzens: Die Grenznutzenkurve
Grenznutzenkurve: Die Kurve zeigt, wie der Grenznutzen in Bezug auf ein Gut von der konsumierten Menge dieses Gutes abhängt. Mathematisch handelt es sich bei der Grenznutzenkurve um die 1. Ableitung der Nutzenfunktion. Sie besitzt eine positive Steigung, mit abnehmendem Verlauf.
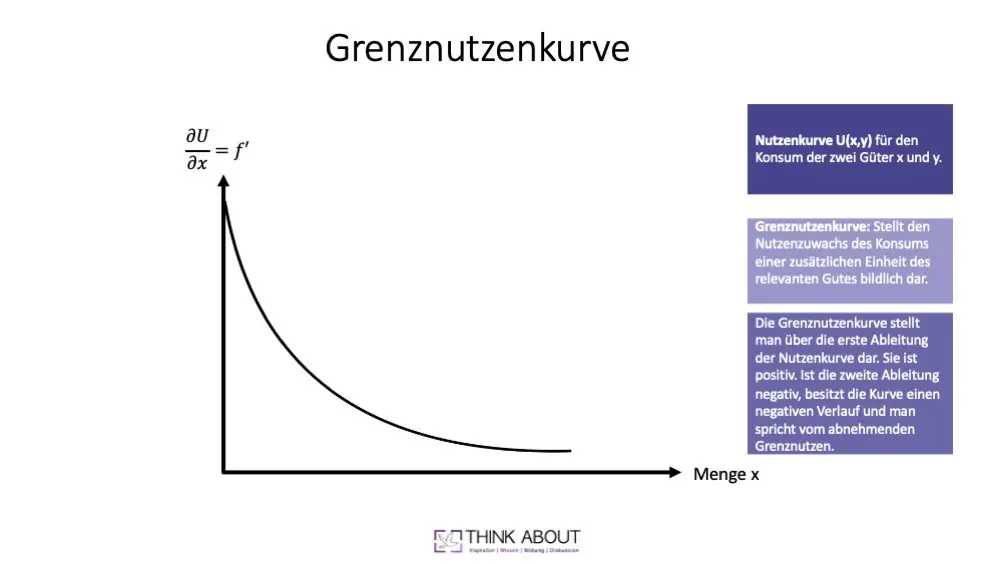
Die Grafik zeigt euch für eine nicht nähere definierte Nutzenfunktion eine Darstellung der Grenznutzenkurve. Ihr erhaltet diese Kurve, wenn ihr -wie im oberen Beispiel- die erste Ableitung der Nutzenfunktion für eines der beiden Güter bildet. Hier setzt ihr dann verschiedene Werte ein und erhaltet die entsprechende Grenznutzenkurve. Die Kurve in dieser Grafik besitzt einen fallenden Verlauf. Entsprechend haben wir hier eine Funktion mit abnehmenden Grenznutzen.
Beispiel: Berechnung und Darstellung konstanter Grenznutzen
Nehmen wir an, wir haben folgende lineare Nutzenfunktion:
U(x,y)=x+6*y
U ist der Nutzen, den der Konsument erzielt
X ist die Menge des ersten Gutes, z. B. ein Glas Sprite
y ist die Menge des zweiten Gutes, z. B. ein Glas Cola
Den Nutzen, den ihr aus dem Konsum jeweils eines Glases erhaltet, berechnet ihr durch Einsetzen:
U(x,y)=1+6*1=7
Jetzt erhöht ihr den Konsum von Cola auf insgesamt zwei Gläser:
U(x,y)=1+6*2=13
Den Nutzenzuwachs, also den Grenznutzen, bildet die Differenz zwischen den beiden Ergebnissen, also 13-7 = 6. Der Grenznutzen beträgt (immer) 6. Würdet ihr y =3 einsetzen, erhaltet ihr U = 19. Und 19–13=6.
Dies war die „intuitive“ Darstellung. Schneller geht es, wenn ihr einfach die Ableitung der Funktion nach y bildet. Dann erhaltet ihr direkt den Grenznutzen von Cola:
\frac{\partial U}{\partial y}=6
Es handelt sich um eine partielle Ableitung. Leitet ihr nach y ab, fällt der Term x weg. Und die Ableitung von 6*y ergibt 6. In Summe ergibt sich damit für die Ableitung 0 + 6 = 6.
Analog könnt ihr den Grenznutzen für Sprite über die partielle Ableitung nach x berechnen:
\frac{\partial U}{\partial x}=1+0=1
Der Grenznutzen für den Konsum von Sprite beträgt damit konstant 1.
In diesem Beispiel erhaltet ihr einen konstanten Grenznutzen für den Konsum beider Güter. D. h. der Nutzenzuwachs bleibt mit steigender Anzahl der konsumierten Menge immer gleich. Ob der Grenznutzen konstant ist oder abnimmt, erhaltet ihr ja über die zweite Ableitung der Funktion:
f'' (y) = 0
Da die zweite Ableitung für Cola = 0 ist, habt ihr auch mathematisch gezeigt, dass der Grenznutzen konstant ist. Würdet ihr als zweite Ableitung einen Wert kleiner 0 erhalten, würde der Grenznutzen abnehmen.
Das vorliegende Ergebnis liegt in der Form der Nutzenfunktion begründet. Im Alltag (oder beim Lernen) dürftet ihr dagegen eher Funktionen begegnen, aus deren Ableitung ein abnehmender Grenznutzen resultiert. So wie bei der anfangs vorgestellten Herleitung anhand einer Cobb-Douglas-Funktion.
Zusammenfassung
Literatur
Weiterführende Informationen zur verwendeten Literatur (Affiliate-Links)
Piekenbrock, D., A. Henning. (Autor)



